Dengesiz Dağılmış Veri ile Çalışma - Oversampling Nedir?

Düzensiz dağılmış bir veri seti üzerinde modelleme yapılırken nelere dikkat etmeliyiz? Tahminleme yaptığımız etiket için yeterli veriye sahip değilsek hangi yöntemleri uygulamalıyız? Etiketlerin önem derecesi aynı değilse modelimizi nasıl oluşturmalıyız? Bu soruların cevaplarını beraber öğrenelim. Bir örnek veriseti ile çalışma yaparken bu sorular için cevap arayacağız ve kullanılan yöntemleri detaylıca inceleyeceğiz.
Bu çalışmada kredi kartındaki fraud (dolandırıcılık) verilerini içeren veriseti ile çalışacağız. Bu veri setinin en önemli özelliği verinin etiketlere düzgün dağılmamış olmasıdır. Farud olmayan verilerin sayısı 284315 tir. Fraud veri sayısı 492 dir. Arada çok büyük bir fark bulunmakta. Verisetimizde fraud olan veri sayısı çok az olmasına rağmen bizim için bu etiketin önemi diğer etikete göre çok daha fazladır. Fraud işlemleri yakalamak bu tür çalışmalarda önceliğimiz olmaktadır. Veri sayısı az, önem düzeyi fazla ve biz bu etikete daha çok odaklanmalıyız. Peki bunu nasıl yapacağız? Hadi projemize başlayalım ve bu sorulara cevap arayalım.
Verisetine buradan ulaşabilirsiniz.
data = pd.read_csv('creditcard.csv')
Verisetimizde eksik veri olup olmadığını kontrol edelim.
data.isnull().sum()

Verisetimizde eksik veri bulunmamaktadır. Çok güzel! Etiketlerin dağılımına bakarak çalışmamıza devam edelim.
data['Class'].value_counts()
0: 284315
1: 492

Verilerin dağılımda çok büyük bir dengesizlik var. Modelleme aşamasına geldiğimizde bu veri dengesizliğinden kurtulmaya çalışacağız. Bu aşamaya gelmeden önce verimizi train, test ve valid verisi olarak ayırıyoruz. Modelimizi train verisi üzerinden eğiteceğiz. Validasyon verimiz eğitim süreci devam ederken modelin durumunu analiz etmemize olanak sağlayacak. Test verisini ise modelimiz eğitim bitene kadar görmeyecek. Bu veriyi modelimizin sonucunu değerlendirme aşamasında kullanacağız. Verimizi üçe bölelim.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.25, random_state=42, stratify=y)
X_test, X_valid, y_test, y_valid = train_test_split(X_test, y_test,
test_size= 0.70, random_state=42, stratify=y_test)
Sıradaki aşama ise verilerimizi standartaştırma aşamasıdır. Veri standartlaştırarak verilerin standart bir forma dönüşmesini sağlayacağız. Bu işlem sonucunda modelimiz verileri daha doğru ve tarafsız bir şekilde değerlendirebilecek. Aynı zamanda verilerimizin boyutu da küçüleceği için modelimiz daha hızlı çalışacak. Bu aşamada StandardScaler yöntemini kullanacağız.
from sklearn.preprocessing import StandardScaler
scaler= StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_valid = scaler.transform(X_valid)
Verilerimizi yukarıdaki kod ile standartlaştırdık. Bu aşamada veri dengesizliği sorununu çözmeye çalışacağız. Verimiz üzerinde oversampling yöntemi uygulayacağız.
Oversampling Nedir, Ne İşe yarar?
Oversampling, verilerin dağılımı düzensiz olduğu zaman verilerin dağılımına müdahale etmemize olanak sağlayan bir yöntemdir. Verisi az olan etiketin verilerini random bir şekilde çoklayarak etiketlerdeki veri sayısını eşitliyoruz. Undersampling ise verisi fazla olan etiketin verilerini random şekilde azaltma yöntemidir. Buradaki amaç da aynı şekilde etiketlerdeki veri sayısını eşitlemektir. Biz projemizde oversampling yöntemini kullanacağız.
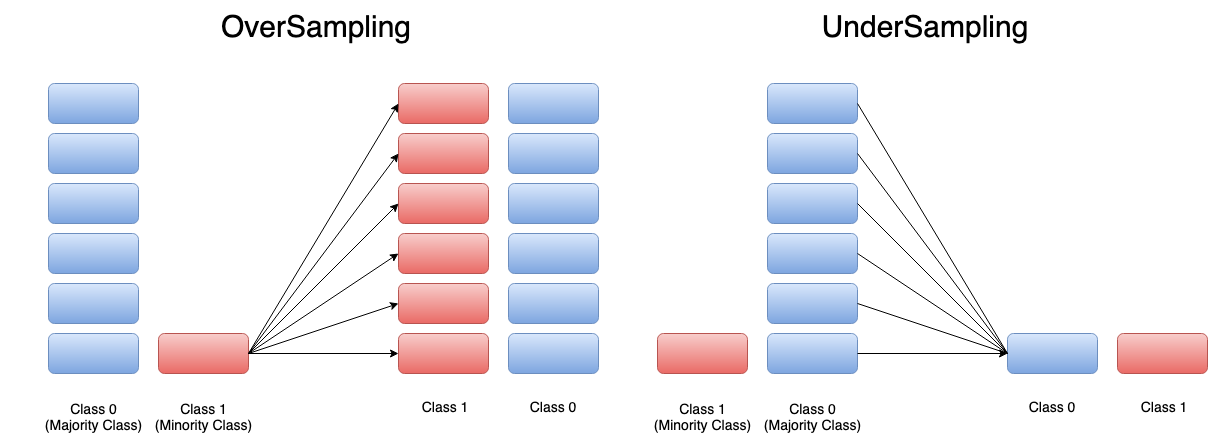
Bu işlemi nasıl uygulayacağımızı beraber inceleyelim.
from imblearn.over_sampling import RandomOverSampler
oversample = RandomOverSampler(sampling_strategy='minority')
X_train, y_train = oversample.fit_resample(X_train, y_train)
RandomOverSampler sınıfını kullanarak bu işlemi çok kolay bir şekilde yaparbiliriz. En az veriye sahip etikete göre verilerin arttırılmasını sağlıyoruz. "sampling_strategy" parametresi ile bu ayarlamayı kolay bir şekilde yapabiliyoruz. Sonraki aşamada ise "fit_resample" metodu ile veriyi arttırmaya başlıyoruz. Buradaki önemli nokta bu işlemi sadece train verisi üzerinde yapıyoruz. Amacımız eğitim aşamasındaki dengesizliği ortadan kaldırmaktır. Validasyon ve test verisi için bu işlemi uygulamıyoruz. Bu veriler olması gerektiği gibi ilk haliyle durmalıdır. Bu sayede sonuçlarımız daha güvenilir olacaktır. Eğitim verimizdeki son duruma bakalım
y_train.value_counts()
0 213236
1 213236
Yukarıda görüldüğü üzere eğitim verisindeki etiketlerin veri sayısını uyguladığımız işlem sonucunda eşitledik..
Verileri temizledik, standartlaştırdık ve veri sayılarını düzenledik. Veri önişleme aşaması burada bitiyor. Sıradaki aşamamız modelleme aşaması. Neler yapacağız beraber inceleyelim.
Model Oluştuma
Bu aşamada belirli modelleme algoritmalarından faydalanacağız. Etiketler için veri sayımızı eşitlemiş olmamıza rağmen yeterli verimi modelden alamayabiliriz. Bu sebeple modelleme aşamasında da dikkat edeceğimiz noktalar olacak. Bu aşamada tek model yerine birden çok modeli (ensemble learning) beraber kullanacağız.
Ensemble Yöntemi Nedir?
Birden çok modelin entegre bir şekilde tahminlemeyi beraber yaptıkları yöntem ensemble yöntemidir. Bu yöntem, modellerin güçlü yönlerini birleştirmemize olanak sağlar. Bu yaklaşım veri dağılımının düzgün olmadığı durumlarda sıkça başvurulan bir yöntemdir. Ayrıca ensemble yöntemi aşırı öğrenme sorununun oluşmasını engelleyebilir ve sonuçların daha stabil olmasını sağlar. Ensemble yönteminin farklı türleri vardır. Projemizde daha az komplex bir ensemble yöntemi kullanacağız. Modelleri ayrı ayrı eğitip bu modellerin tahminlerini birleştireceğiz. Bu yöntem kullanılabileceği gibi modeller beraber de eğitilebilirdi. Bu veriye ve projeye göre değişkenlik gösterebilecek bir durumdur.
Modelleme aşamasında Lojistik Regresyon (Logistic Regression), XGBOOST, KNN (K Nearest Neighbors) modellerini ayrı ayrı kullanıp modellerin sonuçlarını birleştireceğiz.
Lojistik Regresyon Nedir?
Lojistik regresyon ikili sınıflandırmada çok sık kullanılan başarılı bir algoritmadır. Algoritma, hesaplama aşamasında sigmoid fonksiyonunu kullanır. Bu fonksiyon kullanılarak işlem sonucunda verinin hangi sınıfa ait olduğuna dair bir olasılık değeri elde ederiz. Bu olasılık değerlerini kullanarak verilerimizi sınıflandırabiliriz. Aşağıdaki görselde lojistik ve lineer regresyonun verilere nasıl yaklaşıtğını inceleyebilirsiniz.

Bu işlemi pythonda aşağıdaki kod ile kolayca yapabiliriz.
# Model
lr = LogisticRegression(penalty='l2', class_weight = {1:4,0:1}, C=0.001 , max_iter=200)
lr.fit(X_train, y_train)
lr_pred = lr.predict(X_test)
#Sonuçlar
recall: 0.9302325581395349
precision: 0.01773049645390071
accuracy: 0.9109568427599767
f1-score: 0.034797738147020446
Buradaki class_weight parametresi önemlidir. Bu parametre ile "1" (fraud) etiketine sahip verilerin daha önemli olduğunu belirterek modelin bu verileri daha iyi öğrenmesini sağlıyoruz. Modelimizi kuruyoruz, eğitiyoruz, sonrasında ise yukarıdaki sonuçları elde ediyoruz. Modelimiz "1" etiketine sahip verilerin %93 lük kısmını doğru tahmin ediyor. Recall metriği ile bu bilgiye ulaşabildik.
Projemizde kullandığımız diğer algoritma KNN algortimasıdır.
KNN (K Nearest Neighbors) Algoritması Nedir?
KNN algoritması, veriyi sınıflandırmadan önce veriye en yakın komşuların hangi sınıfa dahil olduğunu inceleyen ve değerlendiren bir algoritmadır. Bu inceleme sonucunda yeni gelen verinin hangi sınıfa dahil olacağına karar verir. Bu inceleme aşamasında kaç komşuya bakılacağı önemli bir durumdur. İncelenecek komşu sayısı veriye uygun şekilde ayarlanmalıdır.
Python ile nasıl yapacağımızı beraber inceleyelim.
# Model
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=5,
weights = "distance")
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
#Sonuçlar
recall: 0.813953488372093
precision: 0.7291666666666666
accuracy: 0.9991573202784856
f1-score: 0.7692307692307692
Modelimiz en yakın 5 komşuyu inceliyor. Ayrıca weight parametresine distance değerini verdik. Bu sayede öğrenme ve tahminleme aşamalarında uzaktaki verilerin ağırlığının daha az, yakındaki verilerin ağırlığının ise daha fazla olmasını sağladık. Recall değerimiz önceki modele göre daha düşük geldi. Modelimiz fraud olan verileri tahminlemede ilk model kadar başarılı olmasa da halen güzel sayılabilecek bir orana sahip. Ayrıca "0" etiketini tahminlemede modelimiz yeteri kadar başarılı.
Kullandığımız son algoritma ise XGBOOST algoritmasıdır.
XGBOOST Algoritması Nedir?
XGBOOST algoritması ağaç tabanlı bir algoritmadır. Algoritma verileri sınıflandırıken birden çok ağaç kullanır ve ortak karara göre tahminlemeyi yapar. Bu özelliğinden dolayı XGBOOST algoritması da ensemble modele örnektir.
Aşağıdaki kod yardımıyla bu algortimayı kullanabiliriz.
import xgboost as xgb
# Model
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)
dvalid = xgb.DMatrix(X_valid, label=y_valid)
params = {
"objective": "binary:logistic",
"eval_metric": ['error', 'logloss'],
'n_estimators':2000,
"max_depth":2,
"eta": 0.1,
"gamma": 1,
"subsample": 0.8,
"colsample_bytree": 0.8,
"seed": 1,
"scale_pos_weight" : 10
}
model = xgb.train(
params=params,
dtrain=dtrain,
num_boost_round=100,
early_stopping_rounds=5,
evals=[(dvalid, "Valid")],
verbose_eval=5)
#Sonuçlar
recall: 0.9302325581395349
precision: 0.02075765438505449
accuracy: 0.9241588250637026
f1-score: 0.04060913705583756
"eta" parametresi öğrenme oranını temsil etmektedir. Modelin yeni öğrendiği verilerle kendisini hangi oranda güncelleyeceğini bu parametre ile belirleriz. "scale_pos_weight" parametresi ile etiketlerin önem seviyesini belirledik. "1" etiketinin daha önemli olduğunu belirttik. Validasyon verimizi bu modelde kullandık. Modelimiz belirli bir süre döngü halinde kendini geliştirecek. Bu gelişme aşamasında validasyon verisindeki hata miktarını kontrol edecek ve gelişme olmaması durumunda eğitim sürecini sonlandıracak. Sonuçlara baktığımızda recall değerimizin KNN algoritmasındaki değerden daha iyi olduğu görülmektedir. Accuracy (doğruluk) değerimiz ise lojistik regresyondaki doğruluk değerimizden daha yüksek. XGBOOST modeli ile dengeli bir sonuç elde ettik. Bu durumdan modellerin sonuçlarını birleştirme aşamasında yararlanacağız.
Hadi sonuçları birleştirelim!
Bu aşamada yapacağımız işlem çok basit. Olasılık değerlerinin ortalamasını alacağız. Nasıl yani? Öncelikle basit bir örnek üzeinden inceleyelim.
| Model | Olasılık |
| Model - 1 | 0.60 |
| Model - 2 | 0.45 |
| Model - 3 | 0.15 |
Modellerimiz ve tahmin ettikleri olasılıklar yukarıdaki gibi olsun. Peki sonuç ne olacak?
Sonuç, (0.60 + 0. 45 + 0.15)/3 = 0.40 olarak şekillenecektir. Olasılıkları topladık ve ortalamasını hesapladık.
Tabii ki 3 modelin de eşit şekilde sonucu etkilemesini istemeyebiliriz. Bu durumda elde ettiğimiz sonuçlerı katsayılar ile çarparak modellerin ağırlığını değiştirebiliriz. Bizim projemizde de modeller sonucu eşit şekilde etkilemeyecek. Daha dengeli ve stabil sonuç veren XGBOOST algoritmasının sonuca etkisi diğer algoritmalardan daha fazla olacak.
import numpy as np
# XGBoost
xgb_preds = model.predict(dtest)
# Logistic Regression
lr_preds = lr.predict_proba(X_test)[:, 1]
#knn
y_pred_knn = knn.predict_proba(X_test)[:, 1]
#Ensemble
katsayılar = [3,1,1]
ensemble_preds = np.sum([katsayılar[0] * xgb_preds,
katsayılar[1] * lr_preds,
katsayılar[2] * y_pred_knn], axis=0)/sum(katsayılar)
Modellerimizin sonuçlarını birleştirdik. XGBOOST modelimizin ağırlığını diğer modellerin 3 katı olacak şekilde ayarladık. Son durumdaki oranlarımıza bakalım.
Ensemble recall: % 93.02325581395348
Ensemble precision: % 3.5056967572304996
Ensemble accuracy: % 95.56991232118136
Ensemble f1-score: % 6.756756756756757
Recall oranının %93 te kalmasını sağladık. Bu oranı geliştiremesek de koruyabilmiş olmamız bizim için yeterli bir durumdur. Recall değerini belirli bir seviyede tutarken ensemble yöntem sayesinde accuracy (doğruluk) oranını arttırmayı başardık. Tahminlerimizin nasıl dağıldığını Karışıklık matriksi (confusion matrix) üzerinde de inceleyelim.
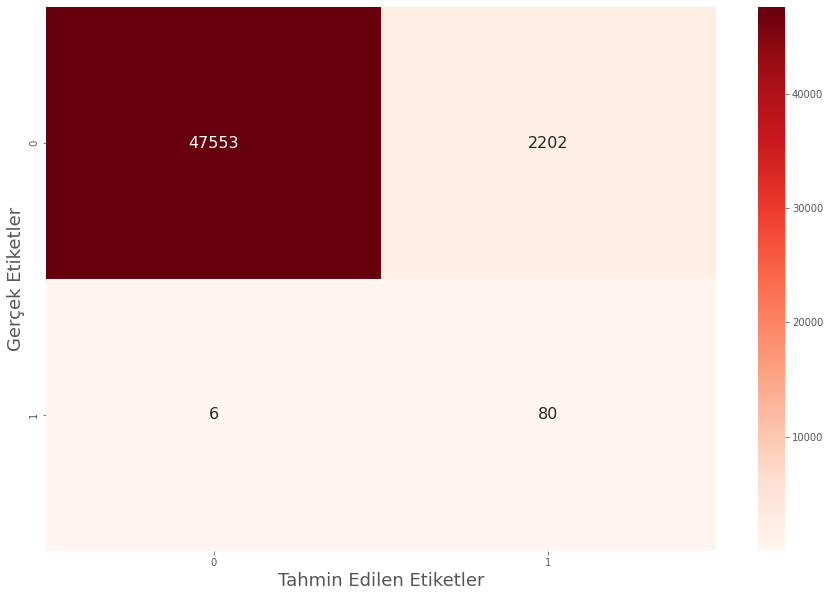
86 tane fraud (dolandırıcılık) verisinden 80 tanesini doğru tahmin ettik. Bu aşamada fraud olmayan 2202 veriye fraud diyerek yanlış tahminde bulunduk. Bu sayı çok fazlaymış gibi görünse de etiketlerin dağılımdaki orantısızlık, "1" etiketindeki veri azlığı ve "1" etiketinin önemi göz önüne alındığında elde edilen sonuç başarılıdır.
Bana ulaşmak ya da takip etmek isterseniz;
Linkedin: www.linkedin.com/in/mustafa-bayhan-410a2a226/
Kaggle : www.kaggle.com/mustafabayhan
Veriseti ve Kod:
Veriseti : www.kaggle.com/datasets/mlg-ulb/creditcardfraud
Kod : www.kaggle.com/code/mustafabayhan/