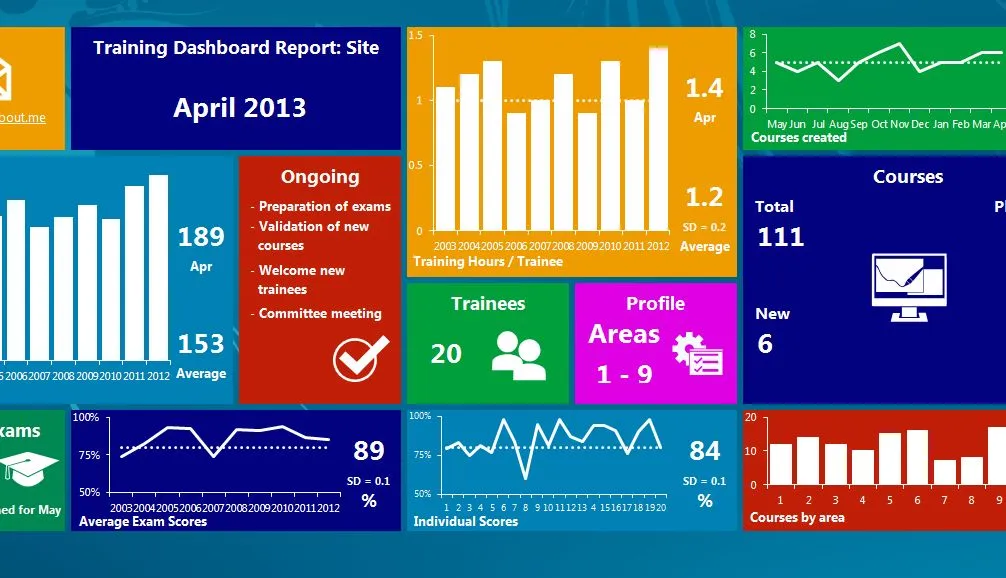
Veri Analizinde Kullanılan Histogram Türleri ve Anlamları

Günlük hayatta ve iş yaşamında sıkça karşılaştığımız veriler, bize önemli ipuçları sunar. Bu verilerin özelliklerini ve dağılımlarını anlamanın en etkili yollarından birisi histogram grafiği kullanmaktır. Histogram, verileri özet haline getirerek verinin dağılımını görselleştirmemize imkan tanıyan istatistiksel bir yöntemdir. Histogram grafiğinin türüne göre verideki simetriyi, çarpıklığı ve uç değerleri yorumlayabiliriz. Histogram ile ilgili detaylı bilgi için Histogram Nedir? isimli yazımı inceleyebilirsiniz.

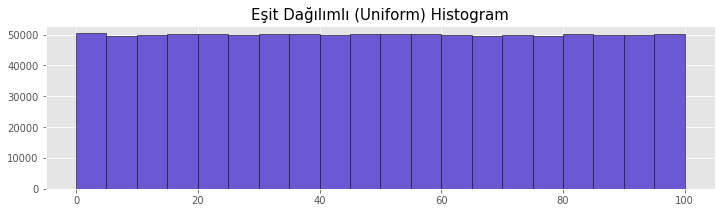
Eşit Dağılımlı (Uniform) Histogram

Eşit dağılımlı histogramda gruplardaki veri sayısının birbiriyle eşit olması beklenmektedir. Deneysellik ve rassallıktan dolayı gruplar arasındaki küçük farklılıklar belirli oranda göz ardı edilebilmektedir. Zar, yazı tura atışı verileri uniform histogram için örnektir.

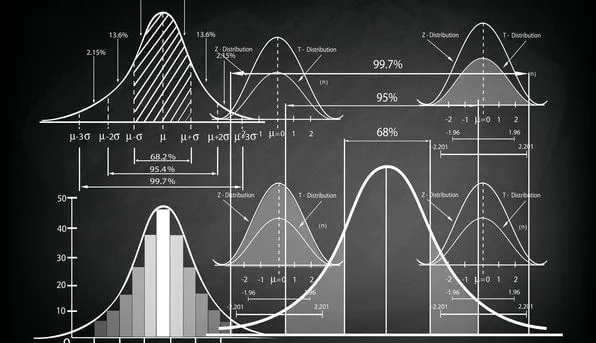
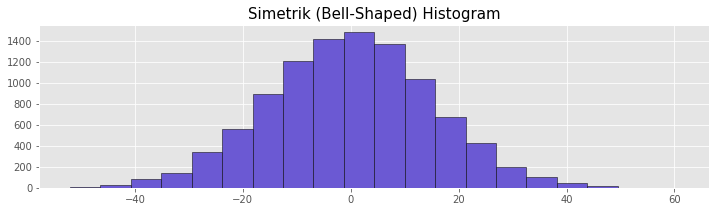
Simetrik (Bell-shaped) Histogram

Simetrik histogramda veri orta noktanın sağına ve soluna simetrik olarak dağılmaktadır. Simetrik histogramda verilerin dağılımı çan eğrisine benzemektedir. Bu tür veriler büyük ölçüde normal dağılıma uyarlar. Özellikle boy uzunluğu gibi belli bir ortalamın etrafında yer alan doğal verilerde bu dağılım sıklıkla görülür. Histogramın yatay uzunluğu üzerinden varyans yorumu yapılabilir. Histogram genişliği arttıkça varyans artmaktadır. Bu da verideki değişikliğin fazla olduğuna işaret eder. 

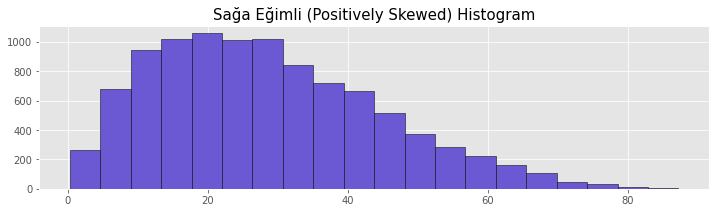
Sağa Çarpık (Positively Skewed) Histogram

Sağ eğilimli histogramlarda tepe noktası grafiğin orta çizgisinin sol tarafında yer almaktadır. Dağılım uzun sağ kuyruğa sahiptir. Bu dağılım sağa eğilimli dağılım olarak da bilinmektedir. Sağa çarpık dağılımlarda Ortalama > Medyan > Mod sıralaması oluşmaktadır. 

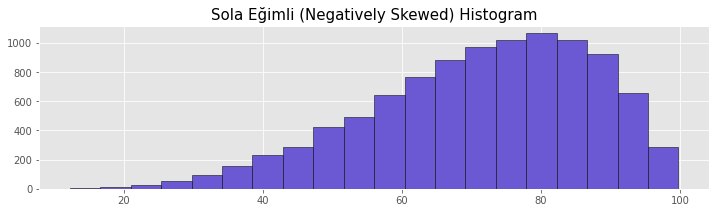
Sola Çarpık (Negatively Skewed) Histogram

Sola çarpık histogramlarda tepe noktası grafiğin orta çizgisinin sağ tarafında yer almaktadır. Dağılım uzun sol kuyruğa sahiptir. Bu dağılım sola eğilimli dağılım olarak da bilinmektedir. Sola çarpık dağılımlarda Mod > Medyan > Ortalama sıralaması oluşmaktadır.

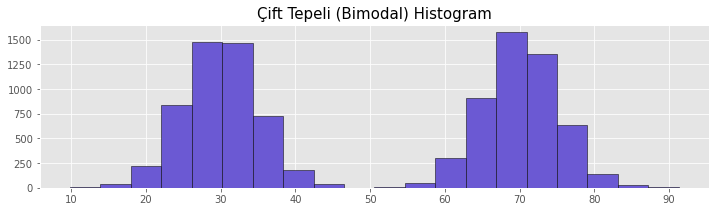
Çift Tepeli (Bimodal) Histogram

Çift tepeli histogramlar iki tepe noktasına sahiptirler. Bu dağılım veri kümesinde birbirinden ayrışan iki grubun olduğunu göstermektedir. Bu dağılım kullanılarak verideki grupların özellikleri incelenebilir ve yorum yapılabilir. Çift tepeli histogramdan elde edilen çıkarımlar ile kümeleme çalışmalarına ve stratejik kararlara ışık tutabilir.

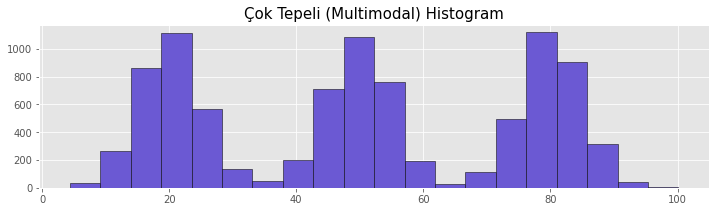
Çok Tepeli (Multimodal) Histogram

Bu histogram türü çift tepeli histograma benzemektedir. Çok tepeli histogramda çok sayıda tepe noktası bulunabilmektedir. Bu durum veri kümesinden birbirinden farklı grupların olduğunu göstermektedir. Homojen olmayan verisetlerinde bu dağılıma sıklıkla rastlanmaktadır. Verisetindeki farklı grupların özelliklerinin incelenmesi ve analiz edilebilmesinde çok tepeli histogramlar önemli bir yere sahiptir.

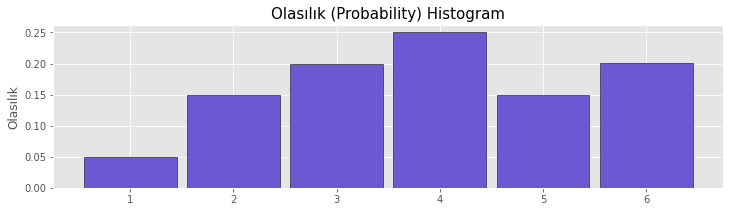
Olasılık (Probability) Histogramı

Olasılık histogramı gruplardaki verinin gerçekleşme olasalığını göstermektedir. Bu sebeple tüm grup değerlerinin toplamı bu histogramda 1 değerine eşittir.

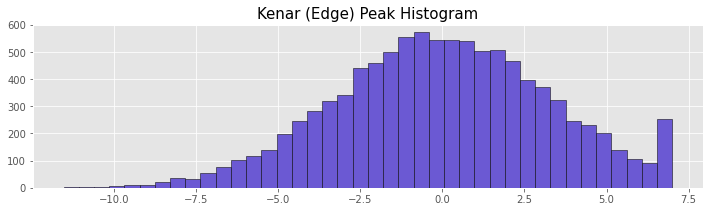
Kenar Peak (Edge Peak) Histogramı 

Bu histogram türünde grafiğin başlangıç ya da bitiş grubunda veri sayısı fazladır. Bu dağılım türünde özellikle kenardaki gruplar incelenmelidir. Kenar Peak histogramı alt ya da üst sınırın yanlış belirlendiğine işaret edebilmektedir.

Yeni çalışmalardan ve benzer içeriklerden haberdar olmak isterseniz beni aşağıdaki hesaplardan takip edebilirsiniz.

Linkedin: www.linkedin.com/in/mustafabayhan/

Medium: medium.com/@bayhanmustafa