Zaman Serisi Analizi (Time Series Analysis) Nedir?

Almak istediğiniz ürünlerin gelecekteki fiyatını bilmek ister miydiniz? Peki yatırım yapacağınız hisselerin gelecekteki değerini bilmek size fayda sağlar mıydı? Şirketinizin gelecek yıl ne kadar satış yapacağını bilseniz ne güzel olurdu değil mi? Peki tüm bunların yapılabileceğini söylesem ne düşünürdünüz? İşte o gizli formül: Zamanda yolculuk, değil tabii ki. Bunları ve çok daha fazlasını yapmamıza olanak sağlayan gizemli formül zaman serisi analizidir. Hadi zaman serilerini beraber inceleyelim!
1. Zaman Serisi (Time Series) Nedir?
2. Zaman Serisi Tahmini Nedir?
3. Zaman Serisi Bileşenleri Nelerdir?
3.1. Trend Bileşeni Nedir?
3.2. Mevsimsellik (Seasonality) Bileşeni Nedir?
3.3. Döngüsel (Konjonktürel) Bileşen Nedir?
3.4. Zaman Serisinde Düzensizlik Etkisi (Noise) Nedir?
4. Zaman Serisinde Durağanlık Nedir?
5. Zaman Serisinde Fark Alma (Differencing) Yöntemi Nedir?
6. Zaman Serisi Analizinde Düzeltme (Smoothing) Teknikleri Nelerdir?
6.1. Basit Üstsel Düzeltme (Single Exponential smoothing) Nedir?
6.2. Çift Üstsel Düzeltme (Double Exponential Smoothing) Nedir?
6.3. Üçlü Üstsel Düzeltme (Triple Exponantial Smoothing) Nedir?
7. Zaman serilerinde tahminleme nasıl yapılır?
8. ACF Yöntemi Nedir, Nerelerde Kullanılır?
9. PACF Yöntemi Nedir, Nerelerde Kullanılır?
10. Zaman serisi tahminleme yöntemleri nelerdir?
10.1. Oto Regresyon - Auto Regression (AR) Yöntemi Nedir?
10.2. Hareketli Ortalama - Moving Avarage (MA) Yöntemi Nedir?
10.3. Otoregresif Hareketli Ortalama (ARMA) Yöntemi Nedir?
10.4. Otoregresif Entegre Hareketli Ortalama (ARIMA) Nedir?
10.5. Mevsimsel Otoregresif Entegre Hareketli Ortalama (SARIMA) Nedir?
10.6. Vektör Oto Regresyon (VAR) Yöntemi Nedir?
10.7. Vektör Otoregresif Hareketli Ortalama (VARMA) Yöntemi Nedir?
10.8. Makine Öğrenmesi Teknikleri ile Zaman Serisi Analizi Nasıl Yapılır?
Zaman Serisi (Time Series) Nedir?
Zaman serileri; zamana göre sıralanan, zamanın değişiminden etkilenen ve birbiriyle ilişkili veriler kümesidir. Bir serideki verinin değeri, kendisinden önceki veriye ve zamanın değişimine göre şekillenir. Zaman serisi analizi çalışmalarında yapılan en yaygın hata, zamana göre kategorize edilen her verinin bir zaman serisi olduğunun düşünülmesidir. Örneğin gün bazında gerçekleştirilen anket sayısını içeren bir veri seti bir zaman serisi değildir. Buna benzer veriler birbirinden ve zamandan bağımsız olarak hareket eder. Bu nedenle zaman serisi analizinde bu ve benzeri veriler genellikle kullanılmaz. Zaman serisi analizi yapılırken verilerin analize uygun olup olmadığına dikkat edilmelidir. Peki zaman serisini oluşturan durumlar nelerdir? Uygun zaman serisi durumlarını birkaç örnekle inceleyelim.
• Hisse senetlerinin değerlerinin zamana göre değişimi
• Bir ürünün fiyatının zamana göre değişimi
• Hava durumu verileri
• Satış verileri
zaman serisine örnektir.
Zaman serisi tahmini (Time Series Forecasting) nedir?
Zaman serisi tahmini, gelecekteki verilerin geçmişteki veriler yardımıyla tahmin edilmesi işlemidir. Bu tahminleme aşamasında geçmişteki veriler çeşitli işlemler uygulanarak değiştirilir ve düzenlenir. Verilere uygulanan işlemler sayesinde gelecekteki verileri tahmin etme aşamasında işimiz kolaylaşacak ve sonuçlarımız çok daha iyi olacaktır. Bu düzenlemelerden en önemlisi veriye uygulanan düzeltmelerdir. Analizde kullanılan düzeltmenin veriye uygunluğu analizin sonucu üzerinde önemli bir etkiye sahiptir. Düzeltme çeşitlerini ve bu düzeltmelerin veriye nasıl uygulandıklarını yazımızın ilerleyen aşamalarında detaylı bir şekilde inceleyeceğiz.
Peki neden zaman serisi verileriyle tahminleme işlemi yapıyoruz? Planlarımızı daha gerçekçi yapabilmek, hedeflerimize ulaşırken avantaj elde edebilmek ve tabii ki de birazcık para kazanabilmek için. Hadi daha yakından inceleyerek zaman serisi analizinin yöntemlerini öğrenelim.
Zaman Serisi Bileşenleri Nelerdir?
1) Trend Bileşeni Nedir?
Trend bileşeni, serideki verilerin belirli bir zaman aralığındaki belirli bir yönde gösterdiği genel eğilimi temsil eder. Trend bileşeni başka bir ifadeyle verilerin belirli bir zaman içinde hangi yönde ve ne şekilde hareket ettiğinin göstergesidir. Aşağıda bir zaman serisi ve verinin genel yönelimi (trendi) gösterilmiştir.
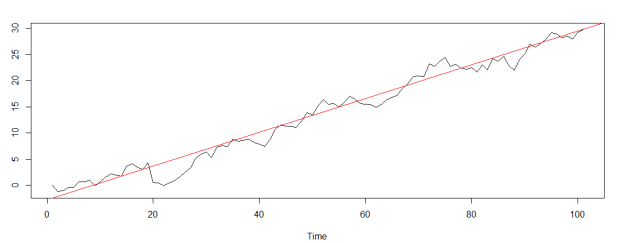
2) Mevsimsellik (Seasonality) Bileşeni Nedir?
Mevsimsellik, zaman değişimin veri üzerindeki etkisidir. Veriler yılın belirli dönemlerinde geçmiş yılların aynı dönemiyle benzer özellikler gösterebilmektedir. Örneğin yaz aylarında soğuk içecek tüketimi artarken kış aylarında düşmektedir. Bu veri her yılın aynı döneminde benzer davranışlar göstermektedir. Bu durum mevsimsellik etkisi olarak bilinmektedir.
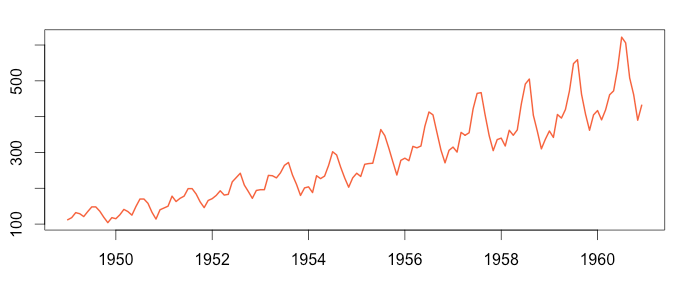
3) Döngüsel (Konjonktürel) Bileşen Nedir?
Döngüsel bileşen, belirli bir olaya ya da karara bağlı olarak oluşan ve veriyi uzun vadede etkileyen durumlardır. Bir yıldan uzun sürebilen bu döngüler genellikle iş dünyasındaki değişimlerin, ekonomik politikaların ve siyasi kararların sonucu olarak oluşurlar. İş döngüsü olarak bilinen refah, durgunluk, depresyon ve iyileşme döngüsü konjonktürel bileşene güzel bir örnektir.
4) Zaman Serisinde Düzensizlik Etkisi (Noise) Nedir?
Verileri etkileyen pek çok dış etken vardır ve bu etkenlerin veri üzerindeki etkileri genellikle düzensizdir. Model tarafından açıklanamayan, verileri tam olarak ne zaman ve ne kadar etkileyeceği bilinmeyen dış etkilerin tamamı düzensizlik etkisi olarak isimlendirilir. Düzensizlik etkisi; deprem, savaş, pandemi gibi öngülemeyen olayların sonucudur. Verideki düzensizlik (Noise), analizin sonucunu doğrudan etkileyen önemli bir faktördür. Analizimizin başarısını arttırmak için verideki gürültü miktarı azaltılmalıdır. Verideki gürültüyü azaltmak için ise sıklıkla Düzeltme (Smoothing) Teknikleri kullanılır. Bu teknikleri yazımızın devamında detaylıca inceleyeceğiz. Zaman serisinde çok önemli bir yere sahip olan Durağanlık (Stationarity) kavramı nedir beraber inceleyelim.
Zaman Serisinde Durağanlık Nedir?
Durağanlık, verilerin belirli bir zaman aralığında istatistiksel değerlerinin değişmemesidir. İncelediğimiz veriler tabii ki bu aralıkta değişkenlik gösterebilir. Önemli olan nokta, verinin bu periyottaki ortalama, varyans ve kovaryans değerlerinin değişmiyor olmasıdır. Bu koşullar sağlanıyorsa veri bu zaman aralığında durağandır. Verimizin durağan olup olmadığını Dickey-Fuller ve Phillips-Perron testleri yardımıyla inceleyebiliriz.
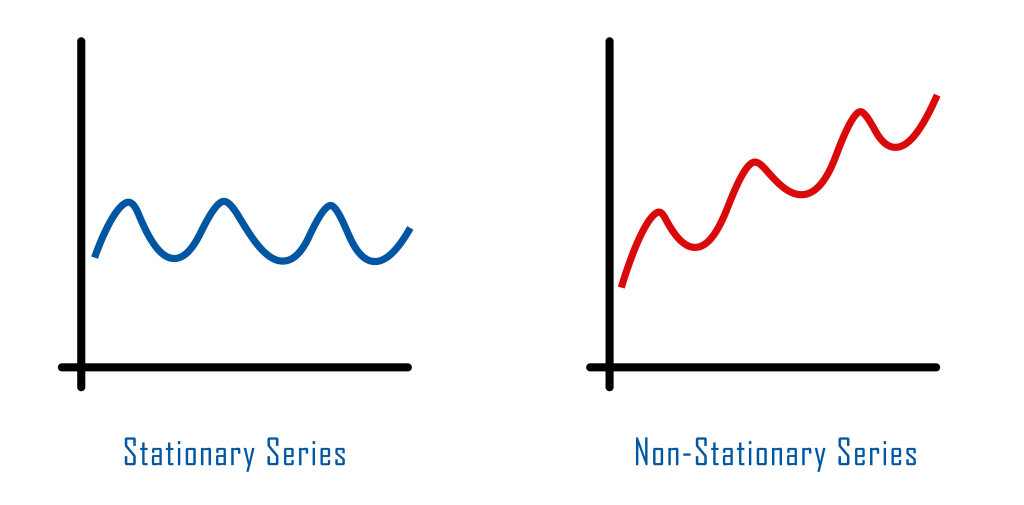
Analize başlarken veri için durağanlık testi yapmalıyız. Eğer verimiz durağan değilse verimizi durağan hale getirmeliyiz. Peki verimizi nasıl durağan hale getireceğiz? Hadi beraber inceleyelim!
Zaman Serisinde Fark Alma (Differencing) Yöntemi Nedir?
Fark alma (Differencing) yöntemi veri durağan olmadığında uygulanan ve veriyi durağan hale getirmeye olanak sağlayan bir tekniktir. Basit ama sık tercih edilen bu yöntemde serideki her veriden kendinden bir önceki veri çıkartılır. Bu işlem sayesinde yeni bir seri elde edilir. Bu elde edilen yeni serinin de durağan olduğu kesin değildir ve yeni seri için de durağanlık testi yapılmalıdır. Eğer veri durağan hale getirildiyse analize bu yeni veri ile devam edilir.
Bu aşamadan sonra verideki gürültüyü azaltmak için neler yapabileceğimizi ve düzeltme tekniklerinin ne işe yaradığını inceleyeceğiz.
Zaman Serisi Analizinde Düzeltme (Smoothing) Teknikleri Nelerdir?
Düzeltme (Smoothing) işlemi veriden gürültüyü uzaklaştırmamıza olanak tanıyan yöntemdir. Modelin verideki açıklayamadığı değişimleri bu yöntemle yumuşatmış, verinin anlamlı parçalarını daha belirgin hale getirmiş oluruz. Sık kullanılan birkaç düzeltme tekniğini beraber inceleyelim.
1) Basit Üstsel Düzeltme (Single Exponential smoothing) Nedir?
Basit üstsel düzeltme, veride trend ve sezonsal etkisi olmadığında kullanılan yumuşatma yöntemidir. Bu düzeltme yöntemi genellikle durağan verilerde daha iyi performans göstermektedir. Hadi bu yöntemi nasıl kullandığımızı inceleyelim!
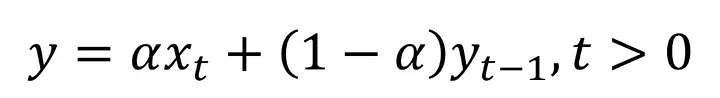
Eğer formül sizi korkuttuysa sakin olabilirsiniz. Henüz korkmamız gereken yerlere gelmedik : )
Karmaşık durmasına rağmen formül basit bir prensibi benimsiyor. Yeni bir tahmin oluştururken işlem yaptığımız verimizin gerçek değeri ile bir önceki verimizin yumuşatılmış halini kullanıyoruz. Peki elimizdeki bu iki sayıdan hangisine daha çok önem vereceğiz? Bu düzenlemeyi alpha parametresi ile yapıyoruz. Bu parametreye 0-1 aralısında bir değer vererek yeni veri için tahminleme yaparken kullandığımız iki verinin katsayılarını düzenlemiş oluyoruz. Bu işlem sayesinde yeni verimizi oluştururken iki veriden hangisini ne oranda kullanacağımızı belirliyoruz. Daha çok karıştı değil mi :) Haydi örnek yaparak inceleyelim!
Serimizdeki 5. değerinin 100 ve yumuşatılmış halinin ise 80 olduğunu varsayalım. Alfa parameresi olarak da 0.3 değerini belirleyelim. Hadi beraber serimizdeki 6. verinin yumuşatılmış halini hesaplayalım.
Y6 = 0.3 * 100 + (1 - 0.3) * 80 = 86
Formülde değerlerimizi yerine yazmaktan başka işlem yapmadık. Bunun sonucunda 6. verimizin gerçek değeri 100 ken yumuşatılmış değerini 86 olarak hesapladık. Bu işlemi serideki tüm veriler için uygularız ve serimizi yumuşatmış oluruz. Bu örnekte bir önceki iterasyondaki yumuşatılmış değerin kaysayısını daha büyük belirlemiş ve sonuca olan etkisini artırmış olduk.
2) Çift Üstsel Düzeltme (Double Exponential Smoothing) Nedir?
Çift üstsel düzeltme yöntemi genellikle veride trend etkisi bulunduğunda kullanılan yumuşatma tekniğidir. Bu düzeltme metodunda verimizin yumuşatılmış halini oluştururken daha önceki aşamadaki verileri kullanıyoruz. Biraz daha komplike olan bu yöntemde iki tane denklem bulunmaktadır. İlk denklem yardımıyla verimizdeki yumuşatma işlemlerini yapıyoruz. İkinci denklem ise yumuşatma işlemine trend etkisini dahil etmemize olanak tanıyor. Bu iki denklemde alfa ve beta isimli birer parametre kullanıyoruz. Bu parametreler 0 - 1 aralığında değerleri alabilmektedir. Bu parametreler yardımıyla yeni tahmin oluştururken hangi veriyi ne oranda kullanacağımızı ayarlayabiliriz. Bir örnekle daha iyi anlayacağız. Hadi örnek yapalım!
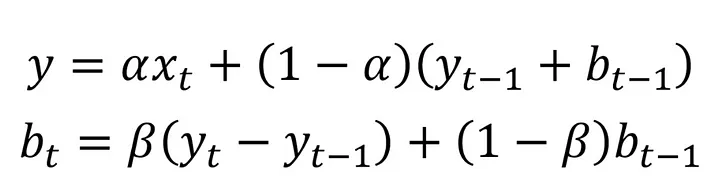
| Aşama | Gerçek X | Yumuşatılmış X | b (trend) |
Alfa |
Beta |
| 5. aşama | 10 | 12 | 4 | 0.3 | 0.4 |
| 6. aşama | 15 | ? | ? | 0.3 | 0.4 |
5. aşamadaki değerleri kullanarak 6. aşamadaki verimizin yumuşatılmış halini ve yeni trend değerimizi hesaplayalım.
y = 0.3 * 15 + (1 - 0.3) * (12 + 4) = 15.7
6. verimizin gerçek değeri 15 ti ve bu verinin yumuşatılmış halini bulmaya çalışıyorduk. Yukarıdaki işlem ile verimizin düzeltilmiş (yumuşatılmış) halini 15.7 olarak hesapladık. Peki trendi nerede kullandık? Bir önceki aşamadaki trend değerimiz (b) 4 tü. Bu değeri denklemdeki yerine yazarak yeni tahmine trend etkisini katmış olduk. İşimiz bitti mi? Tabii ki hayır. Sırada trend denklemimiz için yapacağımız işlemler var. "b" değerimizi güncelleyeceğiz ve bir sonraki aşamada kullanılması için trend değerimizi hazır hale getireceğiz. Hadi yapalım!
b (trend) = 0.4 * (15.7 - 12) + (1 - 0.4) * 4 = 3.88 dir.
Trendineski değeri 4 tü, güncellenmiş değeri ise 3.88 oldu. Yeni trend değerimiz sonraki aşamada kullanılmak için hazır.
Bu iki denklemdeki işlemleri her veri için uygulayarak devam ederiz ve serideki tüm verileri yumuşatmış oluruz.
Bitti sandınız değil mi? Sıkı tutunun daha yeni başlıyoruz.

3) Üçlü Üstsel Düzeltme (Triple Exponantial Smoothing) Nedir?
Holt-Winters'ın üstel düzeltmesi olarak da bilinen üçlü üstsel düzeltme sezonsallık etkisinin olduğu zaman serilerinde kullanılan ve mevsimselliği de tahminlere entegre etmeye olanak tanıyan bir metottur. Aşağıda denklemleri bulunan bu yöntem çok karışık gibi görünse de temelde diğer yöntemlerle benzer özelliklere sahiptir. Bu yöntemde ek olarak mevsimsellik etkisini temsil eden 3. bir denklem bulunmaktadır. Her bileşen (denklem) için bir de parametre (alfa beta ve gama) bulunmaktadır. Bu parametreler ile tahminimizi oluştururken kullandığımız verilerin tahmine hangi oranda etki edeceğini belirlemiş oluruz. Buradaki trend denklemi (2. denklem) ikili üstel düzeltmedeki trend denklemi ile aynıdır. İlk denklemdeki tek fark ise verimizin gerçek değerini sezonsallık değerine (c) bölmemizdir. Bu işlem sayesinde serimizdeki sezonsallığı veriden uzaklaştırmış oluruz. Sezonsallık, verinin belirli zaman periyotlarında benzer davranışlar sergilemesiydi. Bu sebeple sezonsallık değeri güncellenirken belirli bir zaman önceki sezonsallık değeri kullanılır. Bu periyodun uzunluğu verideki sezonsallığın durumuna göre değişkenlik gösterir ve aşağıdaki formulde L sembolü ile temsil edilmiştir. Bir örnek ile incelemeye devam edelim.
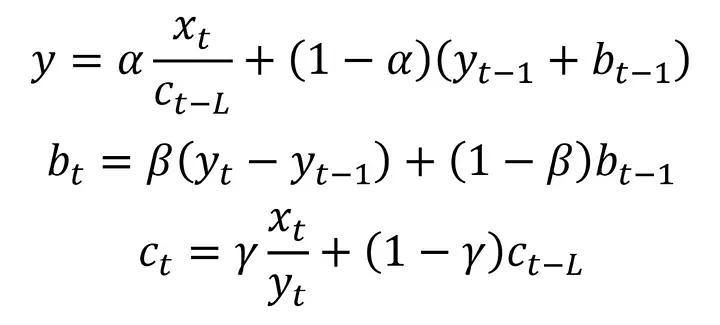
| Aşama | Gerçek X | Yumuşatılmış X | b | c |
Alfa |
Beta | Gama | L |
| 5. aşama | 10 | 12 | 4 | 3 | 0.3 | 0.4 | 0.2 | 2 |
| 6. aşama | 15 | ? | ? | ? | 0.3 | 0.4 | 0.2 | 2 |
Tablodaki değerleri yerine koyarak 6. aşamadaki yeni b (trend), c (sezonsallık) ve yumuşatılmış x değerlerimizi bulalım. İlk denklemimizle işleme başlayalım.
Sezonsallık için periyod uzunluğunu (L) 2 olarak belirledik. Bu sebeple işlemleri yaparken 2 aşama önceki sezonsallık değerini kullanacağız. 6. aşamadaki işlemleri yaparken 4. aşamadaki sezonsallık değerine ihtiyacımız var. Bu değerin 1.2 olduğunu varsayalım.
c4 = 1.2
y = 0.3 * (15 / 1.2) + (1 - 0.3) * (12 + 4) = 14.95 tir.
6. verimizin değeri 15 ti. Yaptığımız yumuşatma işlemi sonucunda ise verimiz 14.95 e dönüştü. Sonraki aşamalarda kullanmak için trend ve mevsimsellik değerlerimizi de güncelleyerek devam edelim.
b = 0.4 * (15.7 - 12) + (1 - 0.4) * 4 = 3.58 dir.
Önceki aşamadaki trend değerimiz (b) 4 tü. Güncellenmiş trend değerimizi ise 3.58 olarak hesapladık. Bu sayede sonraki aşamada kullanacağımız trend değerimiz hazırlamış olduk. 7. verinin yumuşatılmış değerini hesaplarken 4 yerine 3.58 değerini kullanacağız. Çok güzel şimdi de mevsimsellik değerimizi güncelleyelim.
c6 = 0.2 * (15 / 14.95) + (1 - 0.2) * 1.2 = 1.16
4 aşamadaki sezonsallık (c) değerini kullanarak 6. aşamadaki c değerini 1.16 olarak bulduk. Periyod uzunluğumuz 2 birim olduğu için bu hesapladığımız değeri 8. veri için işlem yaparken kullanacağız.
Bu işlemleri serideki her veri için yaparak tüm verileri yumuşatmış ve zaman serisindeki gürültüyü seriden uzaklaştırmış oluyoruz.
Buraya kadar yaptığımız işlemlerde bir şey dikkatinizi çekmiş olmalı. Farkedildiği üzere her aşamada bir önceki verileri kullanarak verimizi yumuşatıyoruz ve değerlerimizi güncelliyoruz. Peki ilk verimizi nasıl yumuşatacağız? İlk veriyi yumuşatırken genelde başlangıç değerlerini kendimiz belirleriz ve işlemlere bu şekilde başlarız. Belirlediğimiz başlangıç değerleri de analizimizin sonucunu etkileyen önemli bir durumdur. Bu sebepten dolayı, başlangıç değeri belirlenirken dikkatli olunmalıdır.
Zaman serilerinde tahminleme nasıl yapılır?
Tahminleme yapma aşamasına geçmeden önce verimiz için durağanlık testi yapılmalıdır ve eğer verimizide gürültü fazlaysa uygun yumuşatma işlemleri uygulanmalıdır. Bu işlemleri yukarıda detaylıca inceledik. Sıradaki aşama ise tahminleme aşamasıdır. Tahmin etmeye çalıştığımız verinin öncesindeki verileri belirli teknikleri kullanarak inceleyeceğiz. Gelecekteki verileri ise bu incelemeler ışığında tahmin etmeye çalışacağız. Peki gelecekteki veriyi tahmin etmeye çalışırken öncesindeki kaç veriyi inceleyeceğiz? Bu veriye göre değişkenlik gösteren bir durumdur. Kaç verinin inceleneceğinin sayısı, gecikmeler (lags) olarak isimlendirilir. Örneğin 7. veriyi tahmin etmeye çalışıyorsak ve gecikme değerimiz 2 ise tahminleme aşamasında 6. ve 5. verimizi kullanacağız. Eğer gecikme değerimiz 3 olsaydı 7. veriyi tahmin ederken 4,5 ve 6. verileri inceleyecektik. Hadi tahminleme tekniklerini inceleyerek devam edelim!
Zaman serisi tahminleme yöntemleri nelerdir?
Oto Regresyon - Auto Regression (AR), Hareketli Ortalama - Moving Avarage (MA), ARMA, ARIMA, SARIMA, VAR ve VARMA gibi istatistiksel yöntemler ile yapay sinir ağları, LSTM gibi makine öğrenmesi teknikleri zaman serileri tahminlerinde sıklıkla kullanılan yöntemlerdir. Bu metotların her birisi detaylıca incelenmesi gereken önemli alanlardır. Kullanılan yöntemin veriye uygunluğu ve modelin doğru parametrelerle kurulması analizin sonucunu etkileyen önemli faktörlerdir. Peki doğru modele ve doğru parametre değerlerine nasıl karar vereceğiz? Modele ve parametrelerine karar verirken çok sık kullanılan iki yöntem ACF ve PACF yöntemleridir. Hadi beraber bu yöntemleri inceleyelim.
ACF Yöntemi Nedir, Nerelerde Kullanılır?
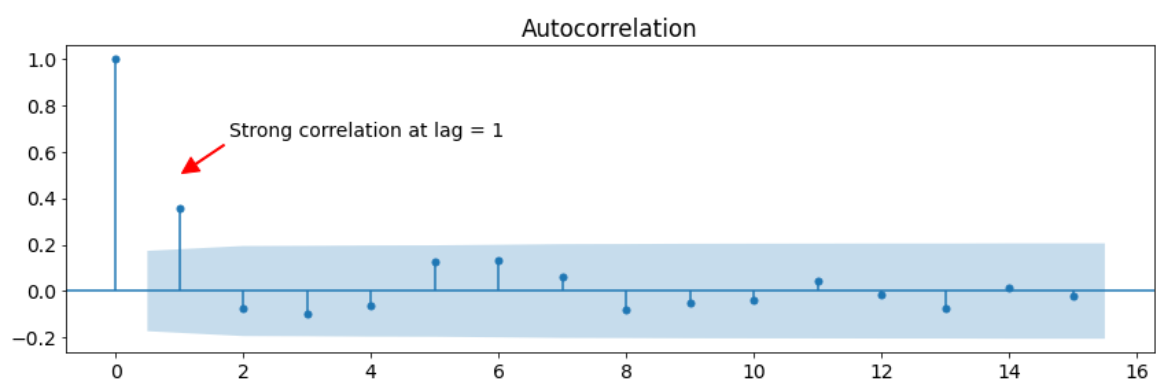
ACF (Autocorrelation Function) gecikme değerlerine göre verideki otokorelasyonu gösteren bir grafik türüdür. Korelasyon iki verinin birbiriyle ilişkisini gösteren ve -1 ile 1 arasında değer alan bir terimdir. Korelasyon değeri 1 e ne kadar yakınsa veriler arasındaki pozitif ilişki o kadar fazladır. Tam tersi durumda değerimiz -1 e yaklaştığındaysa verilerimiz arasında negatif ilişki güçlenmektedir. Korelasyon ile ilgili detaylı bilgi için Korelasyon Nedir? isimli yazımı inceleyebilirsiniz.
ACF yönteminde de bu prensibe göre grafik oluşturulur. ACF grafiği şu anki verimizin geçmişteki verilerle korelasyonunu göstermektedir. Örneğin aşağıdaki ACF grafiğini incelediğimizde şu anki verimizin kendinden öncesindeki 1 veriyle yaklaşık 0.4 korelasyona sahip olduğu görülmektedir. Aynı şekilde şu anki verimiz önceki 6 veriyle yaklaşık olarak 0.2 oranında korelasyona sahipmiş. Gecikme (lag) sayımızı belirlerken bu grafikteki korelasyon değerlerini ve ilişkinin yönünü inceleriz.
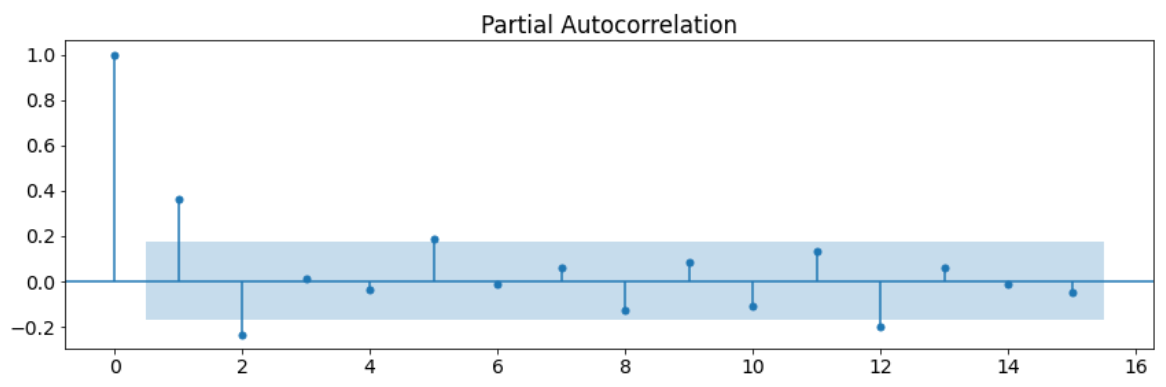
PACF Yöntemi Nedir, Nerelerde Kullanılır?
PACF yöntemi verilerdeki dolaylı ilişkileri göz ardı ederek doğrudan ilişkilerin oranını gösteren bir yöntemdir. Peki doğrudan ilişki ve dolaylı ilişki nedir? Dolaylı ilişki, verilerin birbiriyle başka değişkenler aracılığıyla bağlantıda olmasıdır. Örneğin dondurma satışları ve terlik satışları yaz aylarında artarken kış aylarında azalır. Bu iki veri benzer hareket etmelerine rağmen birbirleriyle doğrudan değil dolaylı olarak ilişkilidir. Bunun sebebi üçüncü bir değişken olan sıcaklık değişkeninin bu iki veriyi birbirine bağlamasıdır. Bu veriler birbirinden değil sıcaklık değişkeninden etkilenirler. Bu ilişki dolaylı ilişkidir. Doğrudan ilişki ise verilerin birbirini direkt etkilemesi durumudur. Aynı örnek üzerinden incelersek sıcaklık ve dondurma satışı doğrudan ilişkiye sahiptir. Sıcaklığın değişimi dondurma satışını direkt etkilemektedir. PACF yöntemi ile şu anki verimizle geçmişteki verilerin doğrudan ilişki oranlarını tespit etmiş oluruz. PACF grafiğinde de ACF grafiğinde olduğu gibi farklı gecikme değerleri için hesaplanmış korelasyon değerleri bulunmaktadır. Bu grafikteki değerlere göre gecikme sayımızın kaç olması gerektiğini belirleyebiliriz. Aşağıda örnek bir PACF grafiği bulunmaktadır.
Bu iki yöntemi hem doğru parametre değerlerine hem de veriye uygun modele karar verirken kullanabiliriz. İki grafiğin karşılaştırılması ve bu grafiklerdeki değerlerin analizi sonucunda hangi modelin kullanılacağına karar verebiliriz.
Sıradaki aşamamız zaman serisi tahminleme yöntemleridir. Asıl oyun şimdi başlıyor :)

Zaman serisi tahminleme yöntemleri nelerdir? Hadi gelin beraber inceleyelim!
1) Oto Regresyon - Auto Regression (AR) Yöntemi Nedir?
Oto Regresyon yöntemi, verilerin kendinden önceki verilerle ilişkisinin doğrusal (lineer) bir model ile açıklanabileceği varsayımına dayanan bir metottur. Verilerin birbiriyle olan ilişkisinin lineer bir modelle açıklanabilmesi için verilerin korelasyonu, başka bir ifadeyle birbirlerine olan bağlılıkları fazla olmalıdır. Mevsimsellik etkisinin, trendin ve gürültünün verilerin birbiriyle olan ilişkisini azalttığını, verinin anlamlı özelliklerini değiştirdiğini öğrenmiştik. Bu sebeple oto regresyon yöntemi; mevsimselliğin, trendin ve gürültünün olmadığı tek değişkenli zaman serilerinde kullanılmaktadır.
2) Hareketli Ortalama - Moving Avarage (MA) Yöntemi Nedir?
Hareketli Ortalama, gelecektaki verinin geçmişteki verilerin ortalamasına yakın olacağı varsayımına göre hareket eden bir tahminleme yöntemidir. Bu yöntemde her veri için geçmişe yönelik belirli sayıdaki verinin ortalamasını alarak serimizin genel hareketini anlamaya çalışacağız. İşlem yaptığımız veri değiştikçe ortalaması alınan aralık da değişecektir. Örneğin önceki 2 veriye bakarak analizimizi yapıyorsak 7. veriyi tahmin ederken 5 ve 6. sıradaki verimizin ortalamasını alırız. Sonraki aşamada 8. veri için işlem yaparken 6 ve 7. verinin ortalamasını alırız. Ortalaması alınan aralık hareket ettiği için bu yöntem hareketli ortalama olarak isimlendirilir. Kaç verinin ortalamasının alınacağı veriye ve analizin amacına göre değişecektir. Küçük aralıkların ortalaması alınarak yapılan tahminlemeler daha kısa vadeli tahminler olacaktır. Verinin uzun vadeli durumunun tespit edilebilmesi için ise analiz aşamasında daha geniş pencere aralığının (lag - gecikme) ortalaması alınmalıdır.
3) Otoregresif Hareketli Ortalama (ARMA) Yöntemi Nedir?
Otoregresif Hareketli Ortalama (ARMA), hareketli ortalama ve oto regresyon tekniklerinin birleştirilmiş şeklidir. ARMA yöntemi hem gelecekteki verileri hem de gelecekteki hataları aynı anda tahminlemeyi amaçlayan bir tekniktir. Modelin içeriğindeki oto regresyon (AR) bileşeni ile gelecekteki değerlerin tahminlemesi yapılırken hareketli ortalama (MA) bileşeni ile de gelecekteki hatalar tahminlenir. ARMA modeli iki parametre alır ve ARMA(p,q) şeklinde gösterilir. "p" parametresi gelecekteki veriler tahminlenirken geçmişteki kaç verinin dikkate alınacağını temsil eder ve oto regresyon bileşeni tarafından kullanılır. "q" parametresi ise gelecekteki hataların tahminlenmesi yapılırken geçmişteki kaç hata değerinin dikkate alınacağını temsil eder ve hareketli ortalama bileşeni tarafından kullanılır. Başka bir ifadeyle, "p" parametresi veriler için gecikme (lag) sayısı temsil ederken "q" parametresi ise hata değerleri için gecikme sayısını temsil eder. Örneğin ARMA(3,2) modeliyle 7. veriyi ve hatayı tahminlemeye çalıştığımızı varsayalım. Veriyi tahminlerken 4,5, ve 6. veriler kullanır ve tahminimizi oluştururuz. Hatayı tahminlerken ise 5 ve 6. verilere ait hata değerleri kullanılır ve hata tahmini oluşturulur. Bu iki tahmin beraber değerlendirilerek daha kapsamlı bir analiz sonucu elde edilir.
4) Otoregresif Entegre Hareketli Ortalama (ARIMA) Nedir?
ARIMA, seriyi durağan hale getirmek için fark alma işlemi uygulanan ARMA modelidir. Fark alma işleminde her veriden bir önceki veriyi çıkarıp yeni bir seri elde edildiğini incelemiştik. Bu işlemi kaç kere yapacağımızı ise ARIMA modelinde belirleyebiliriz. "d" parametresi fark alma derecesi olarak da isimlendirilir ve seride fark alma işleminin kaç kere yapılacağını belirtmemize olanak sağlar. Bu işlemden sonrası ARMA modeli ile aynıdır. Fark alma işlemi sonucunda elde edilen seride gelecek verileri tahmin ederken hem veri değerleri hem de hata miktarları tahmin edilmeye çalışılır. ARIMA modelinin parametreleri aşağıdaki gibi sembolize edilir.
ARIMA(p, d, q): AR(p) + I(d) + MA(q)
5) Mevsimsel Otoregresif Entegre Hareketli Ortalama (SARIMA) Nedir?
Mevsimsel Otoregresif Entegre Hareketli Ortalama (SARIMA) modeli, mevsimsellik bileşenini içeren bir ARIMA modelidir. SARIMA modeli hem ARIMA modelinin parametrelerini hem de sezonsallık bileşeninin parametrelerini içerir. SARIMA modelini aşağıdaki gibi sembolize edebiliriz.

Hadi buradaki parametreleri beraber inceleyelim!
m parametresi: Serideki mevsimsel döngünün ne kadarlık sürede tamamlandığını bu parametre ile belirleriz. Örneğin verimiz aylık bir veriyse ve yıllık bir döngüye sahipse m parametremizin değeri 12 olur. Bu örnekteki verimiz her yılın aynı ayında benzer davranışlar gösterecektir. Örneğin her yılın ocak ayındaki harekterler birbirine benzer olacaktır. Hadi bu örnek üzerinden diğer sezonsallık parametrelerini de inceleyelim.
P parametresi, Oto Regresyon (AR) ile veri tahminlemesi yapılırken geçmişteki kaç sezona ait verinin inceleneceğini belirleyebildiğimiz parametredir. Örneğin P parametresi 3 ise ve ocak ayı için tahmin yapıyorsak geçmiş 3 yıla ait ocak ayı verileriyle işlem yaparız.
D parametresi, fark alma işleminin kaç kere yapılacağını belirleyen parametredir. Fark alma işlemi yapılırken şu anki veriden bir önceki sezondaki ocak ayı değeri çıkartılır. Örneğin D parametresi 2 ise Ocak ayındaki değerden bir önceki ocak ayındaki değeri çıkararak yeni bir ocak ayı serisi elde etmiş oluruz. Bu 1. işlemdir ama bizim fark alma derecemiz ikiydi. Yeni elde ettiğimiz ocak ayı verisine tekrar fark alma işlemi uyguladığımızda ocak ayı için sonuca ulaşmış olacağız. Bu işlemleri diğer sezonlar için de uyguladığımızda tüm veriyi durağan hale getirmiş oluruz.
Q parametresi, Hareketli Ortalama (MA) ile hata değeri tahminlenirken geçmişteki kaç sezona ait kaç hata değerinin inceleneceğini belirleyen parametredir. Örneğin bu değer 4 ise ve yine ocak ayı için hata tahmini yapıyorsak geçmiş 4 yılın ocak aylarına ait hata değerlerini kullanırız.
Verimizin 12 aylık sezonsal döngüye sahip olduğunu varsayarak bu örnekleri yaptığımıza dikkat edilmelidir. Eğer verimiz 4 aylık döngüye sahip olsaydı bir öceki sezon olarak 12 ay önceki verileri değil 4 ay önceki verileri kullanacaktık.
6) Vektör Oto Regresyon (VAR) Yöntemi Nedir?
Vektör Oto Regresyon (VAR) yöntemi, Otoregresyon (AR) yönteminin birden çok değişken (boyut) için kullanılan halidir. VAR modeli AR modeli ile aynı prensibleri benimser. Aralarındaki tek fark, VAR yönteminin bu prensibleri çok değişkenli modellere uygulamasıdır.
7) Vektör Otoregresif Hareketli Ortalama (VARMA) Yöntemi Nedir?
Vektör Otoregresif Hareketli Ortalama (VARMA) yöntemi, ARMA yönteminin birden çok değişken için kullanılan halidir. VARMA yöntemindeki prensip ve yöntemler ARMA modeli ile aynıdır. Aralarındaki tek fark VARMA yönetminin çok değişkenli modeller için kullanılmasıdır.
8) Makine Öğrenmesi Teknikleri ile Zaman Serisi Analizi Nasıl Yapılır?
Makine öğrenmesi teknikleriyle zaman serisi analizi yapılırken de temel prensip aynıdır. Durağan hale getirdiğimiz veriyi makine öğrenmesi algoritmalarına girdi olarak veririz. Bu algoritmalar çeşitli istatistiksel prensiplere göre veriyi inceler ve verideki değişimleri analiz ederek verinin yapısını öğrenir. Makine öğrenmesi algoritmalarının birbirinden farklı avantajları ve dezavantajları vardır. Bu sebeple hangi algoritmanın kullanılacağı analizin sonucu için önemlidir.
Zaman serilerinde bu yöntemler dışında başka yöntemler de vardır fakat genel itibariyle en çok kullanılan ve en iyi sonuç veren yöntemler bunlardır. Artık gelecekteki verilerimizi bilimsel temellere göre inceleyebilir planlarımızı bu sonuçlara göre yapabiliriz. Benzer içerikleri kaçırmamak için aşağıdaki hesaplarımı takip edebilirsiniz.
Linkedin: www.linkedin.com/in/mustafabayhan/
Medium: medium.com/@bayhanmustafa
Kaggle : www.kaggle.com/mustafabayhan
Buraya kadar beraber geldik. Bir kutlamayı tabii ki hak ettik.