
What is Artificial Neural Networks, How Does It Work?

HadYapay Sinir Ağları (YSA) insan beyni gibi çalışan bir derin öğrenme algoritmasıdır. Katmanlardan, nöronlardan ve bu nöronlar arası bağlantılardan oluşan yapay sinir ağlarının en büyük avantajı bu sinirsel bağlantılara belli oranda müdahele edilebilmesidir. Peki ama katman nedir? YSA nın yapısındaki tüm nöronlar birbirine bağlı değildir. Nöronlar katmanlar halinde dizilidir ve bir katmandaki (ara katman) nöron ancak kendinden önceki ve kendinden sonraki katmanlarla bağlantıdadır. Görsel üzerinde bunu açıklamak daha yararlı olacaktır.
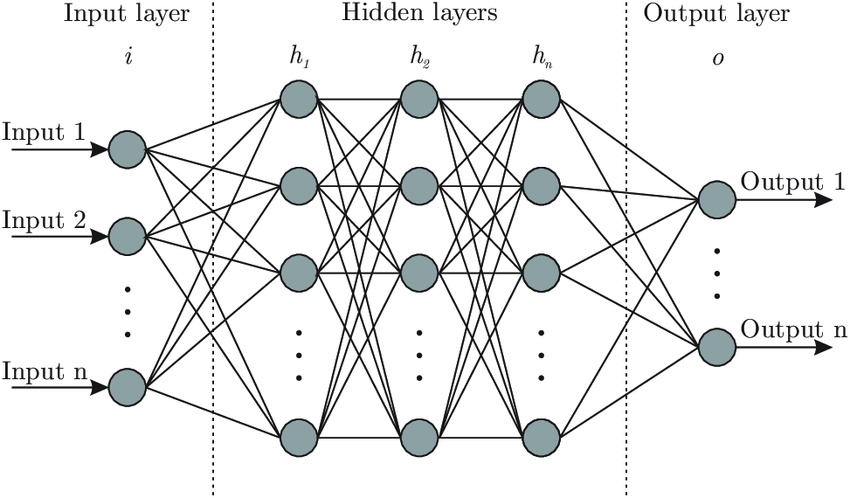
Algoritma giriş katmanı ile veriyi alır. Katmandaki her nöron kendinden sonraki katmandaki her nörona veri gönderir. Çıkış katmanı sayesinde de algoritma öğrendiği sonucu dış ortama yansıtır.
Sinir hücreleri nasıl çalışır?
Her hücrenin sonuca etkisi aynı değildir. Hücreler belirli oranda sonuca katkı sağlar. Bu oranlara hücrelerin ağırlığı (w) denir. Hücreye ulaşan veriler o hücrenin ağırlığı ile çarpılır ve sonuçlar toplanır. Bu işlem ile birlikte elde edilen değere bir bias (b) değeri eklenir. Bias model için hata miktarı olarak düşünülebilir. Bias ekleyerek modelin esnek olmasını sağlasak da bu hatanın optimum seviyelerde olması tercih edilir.
nöron çıktısı = W * X + b denklemine ulaştık
W = Nöron ağırlığı
X = Gelen veri
b = bias
Nöron ağırlığı nasıl hesaplanır?
Yapay sinir ağlarındaki temel amaç buradaki bias ve ağırlık için optimum değerleri bulmaktır. Bunun için de optimizasyon fonksiyonları kullanılır. Fakat burada önemli bir nokta var. Optimize etmemiz için başlangıçta elimizde w değerleri olması gerekir. Bu w değerleri rastgele belirlenebilir. Algoritma çalıştıkça bu değerler değişecek ve optimum noktaya yaklaşacak. Rastgele ağırlık değerleri belirlenirken negatif ve pozitif sayılardan seçilmelidir. Sıfır değeri ağırlık olarak verilirse güncelleme yapılamayacaktır.
Peki buraya kadar geldik şimdi ne yapacağız? Hücre dışarıya bir veri gönderiyor. Bu veriyi değerlendirmemiz ve aktivasyon fonksiyonuyla dönüştürmemiz gerekir.

Peki neden bu dönüşüme ihtiyaç duyuyoruz? Hücreden çıkan veri direkt aktarılırsa algoritma basit linear regresyondan farksız olacaktır. Gerçek veriler genellikle kompleks yapıdadır ve bir çok dönüşüm gerektirir. Nörondan çıkan veri sonraki aşama için anlamlı ve uygun olmalıdır. Örnek vermek gerekirse bir sınıflandırma çalışması yaptığımızı ve kanserli hücre ile kansersiz hücreyi ayırt etmeye çalıştığımızı düşünelim. Çıkış katmanına ikili sınıflandırmaya yarayan adım (step) fonksiyonunu koyarak veriler belirli bir değerin üstündeyse sonucun 1, değil ise 0 olmasını sağlayabiliriz. Bu sayede nöronlardan gelen değerler sonraki aşama için dönüştürülmüş oldu.
Çok kullanılan aktivasyon fonksiyonlarından birkaç tanesi resimde bulunmaktadır. Bu fonksiyonların avantajları dezavantajları ve ne zaman kullanılacakları algoritmanın başarısını önemli derecede etkiler. Fonksiyonların özelliklerini anlamak için bu gönderiyi incelemek faydalı olacaktır.
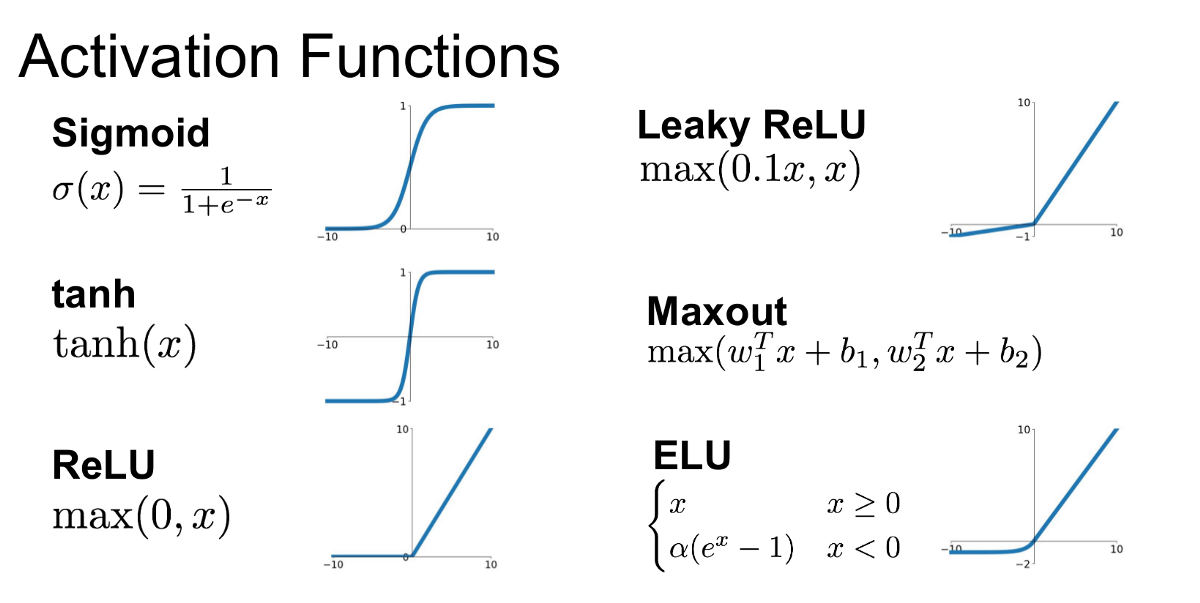
Bu aşamadan sonra çıktı aşaması gelir. Eldeki veriler katmanlardan ve aktivasyon fonksiyonlardan geçerek sonuca ulaşır. Peki burada bitiyor mu? Tabii ki hayır! En önemli aşama başlıyor. Tahminlerimiz (çıktı verileri) ile gerçek sonuçlar karşılaştırılarak loss değeri hesaplanır. Loss değeri bir hata değeri olarak düşünülebilir. Algoritmadaki parametreler güncellenerek bu lost değeri minimize edilmeye çalışılır. Hadi birkaç yeni terimle tanışalım. Optimizasyon fonksiyonları, hata metrikleri (loss) ve epoch. Loss fonksiyonları aracılığıyla kurulan modelin başarısı değerlendirilebilir. Aktivasyon fonksiyonlarında olduğu gibi burda da loss fonksiyonlarını tanımak ve doğru fonksiyonu kullanmak algoritma için önemlidir. En çok kullanılan hata metrikleri MSE, RMSE, MAE ve MAPE dir. Bunların formülleri aşağıdaki gibidir. Tabii ki diğer hata metriklerini ve bu metriklerin detaylarını bilmek avantaj sağlayacaktır. Diğer metrikler ve metriklerin detayları için bu sayfayı inceleyebilirsiniz.

Sırada bu hatayı minimize etmek var. İşte bu aşamada optimizasyon algoritmaları ve epoch kavramı devreye giriyor. Verilerin nöronlardan geçerek sonuca ulaşması ve parametrelerin güncellenerek başa dönmesi 1 epoch kabul edilir. Tur sayısı ya da döngü sayısı olarak düşünülebilir. Bu aşamadaki en önemli nokta doğru optimizasyon algoritmasını seçmektir. Algoritma seçilirken algoritmanın veri setine uygunluğu, hızı, verimi gibi özellikleri dikkate alınmalıdır. Aşağıdaki resimde algoritmaların hata miktarını zamanla düşürdükleri görülmektedir.
Bu algoritmaların hepsinin kendi içinde önemli noktaları vardır ve detaylıca incelenmelidir. Genel mantığı anlamak için gradient descent algoritmasını temel düzeyde inceleyelim.
Bu konuyla ilgili detaylı bir post yazmayı ve bu algoritmaları açıklamayı düşünüyorum. Şimdilik genel mantığı anlamak burada yeterli olacaktır. Detaylı incelemek isteyenler bu posta göz atabilirler.
Öncelikle parametreyi güncellerken kullandığımız denklemi yazalım.
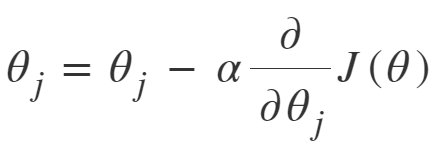

Bekle, dur! Göründüğü kadar zor değil. Yaptığımız temel şey loss fonksiyonunun türevini alıp bunu öğrenme oranıyla çarpmak ve sonra da güncellenecek parametreden bu hesapladığımız değeri çıkarmak. Soru işaretlerini görür gibiyim. Haydi adım adım gidelim.
Öğrenme oranı (learning rate) nedir?
Eğtim sürecinde parametrelerin hangi oranda güncelleneceğini belirleyebiliriz. Yeni öğrenilen verilerin eski verileri ne oranda geçersiz kılacağını, hataların hangi oranda güncelleneğini modeldeki hiper parametrelerden birisi olan öğrenme oranı ile belirleriz. Bu sayede modelin öğrenme hızını belirlemiş oluruz. Çok güzel! model kendini çıktıya göre güncelliyor, kendini geliştiriyor ve veriyi öğreniyor peki neden bunu belli bir oranda yapmaya zorluyoruz? Bunun temel nedeni optimal değere ulaşmaya çalışmamızdır ve öğrenme belli oranlarla gerçekleşmezse bu optimal değeri bulma ihtimalimiz azalacaktır. Aşağıdaki görsel üzerinde bu daha net görülecektir.
Grafik hata fonksiyonuna ait ve biz minimum hatayı bulmaya çalışıyoruz. Öğrenme oranı yüksek olursa model sonuçtan çok etkilenecek ve ikinci grafikteki gibi büyük değişimler olacaktır. Büyük öğrenme katsayısı olduğunda muhtemelen minimum hataya ulaşılamayacak ve sonuç istediğimiz gibi olmayacaktır. Bir dakika! Bu katsayı çok küçük olursa ne olacak? Bu sefer minimum hataya ulaşma ihtimalimiz artacaktır fakat öğrenme yavaş olduğu için daha çok zamana ihtiyacımız olacaktır. Minimum hataya ulaşmak için gereken iterasyon (her güncelleme bir iterasyon demektir) sayısı fazla olacaktır. Bu da büyük verilerle çalışırken dezavantajımıza olan bir durumdur.
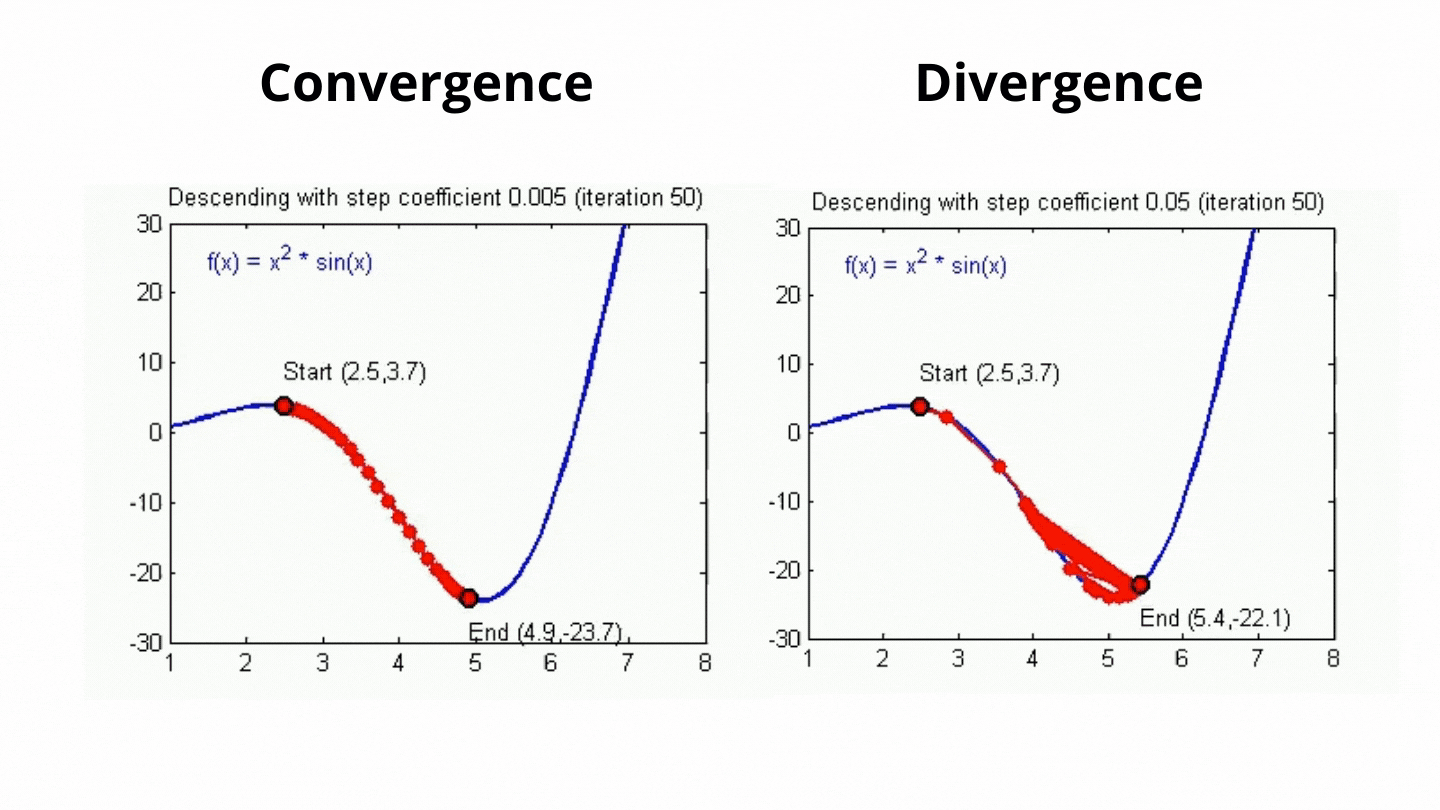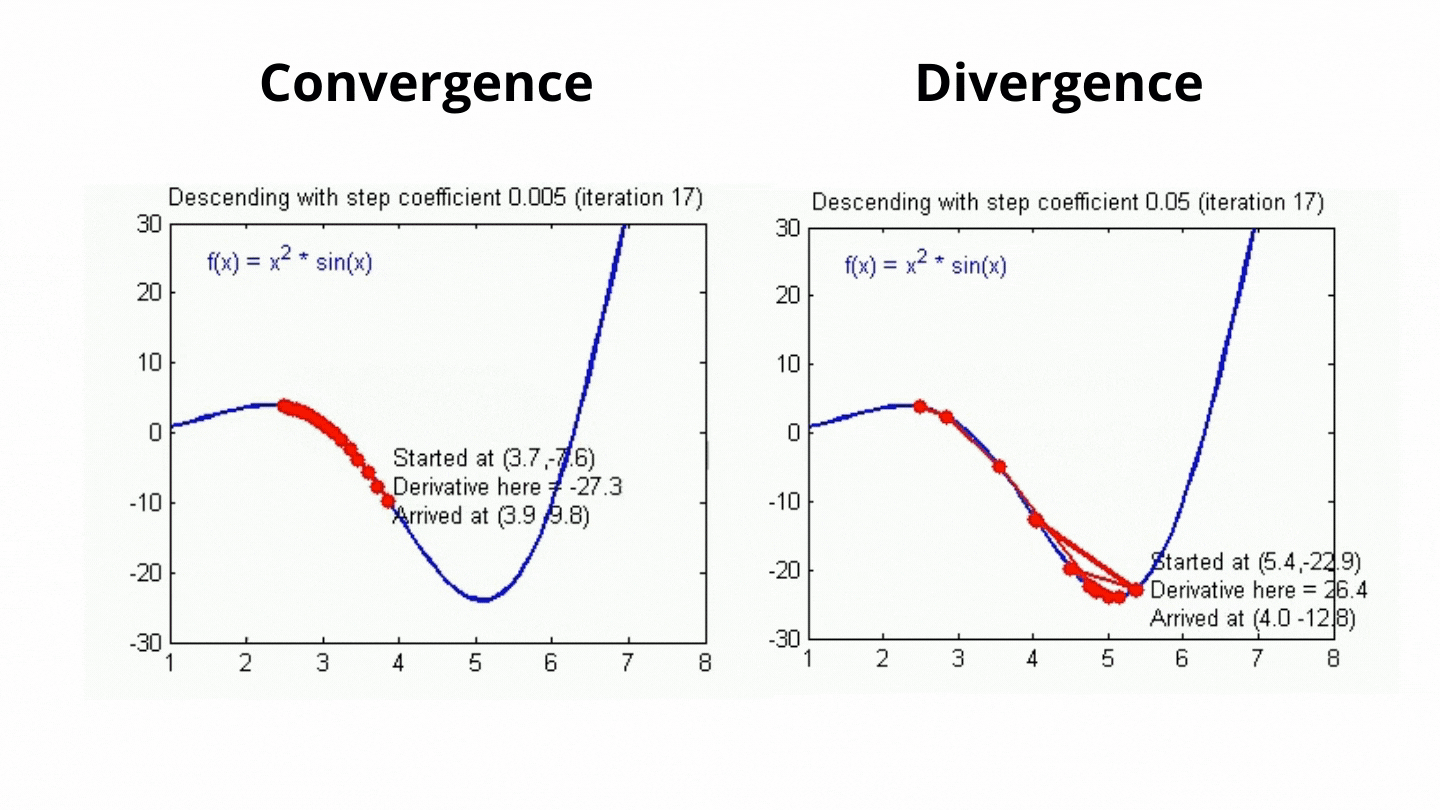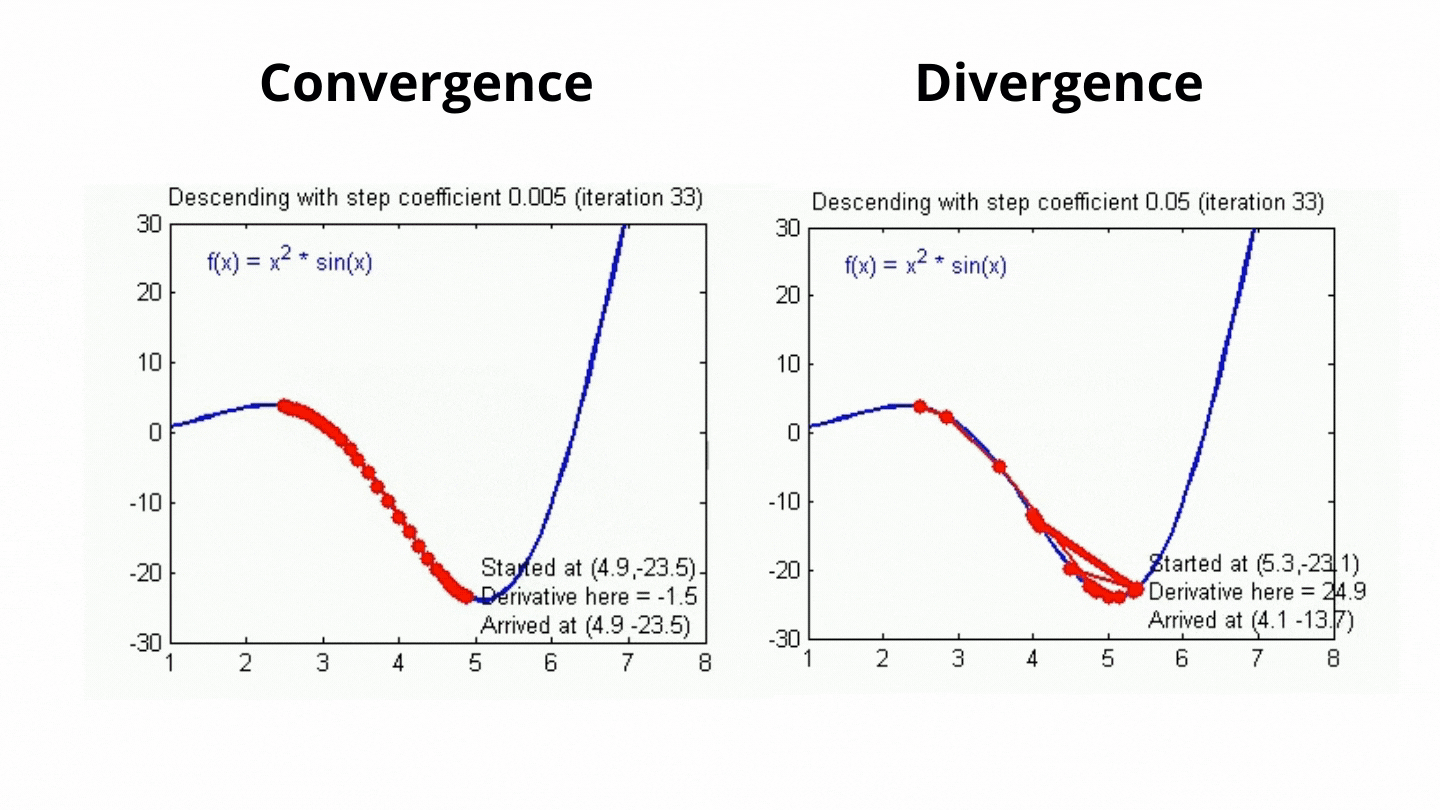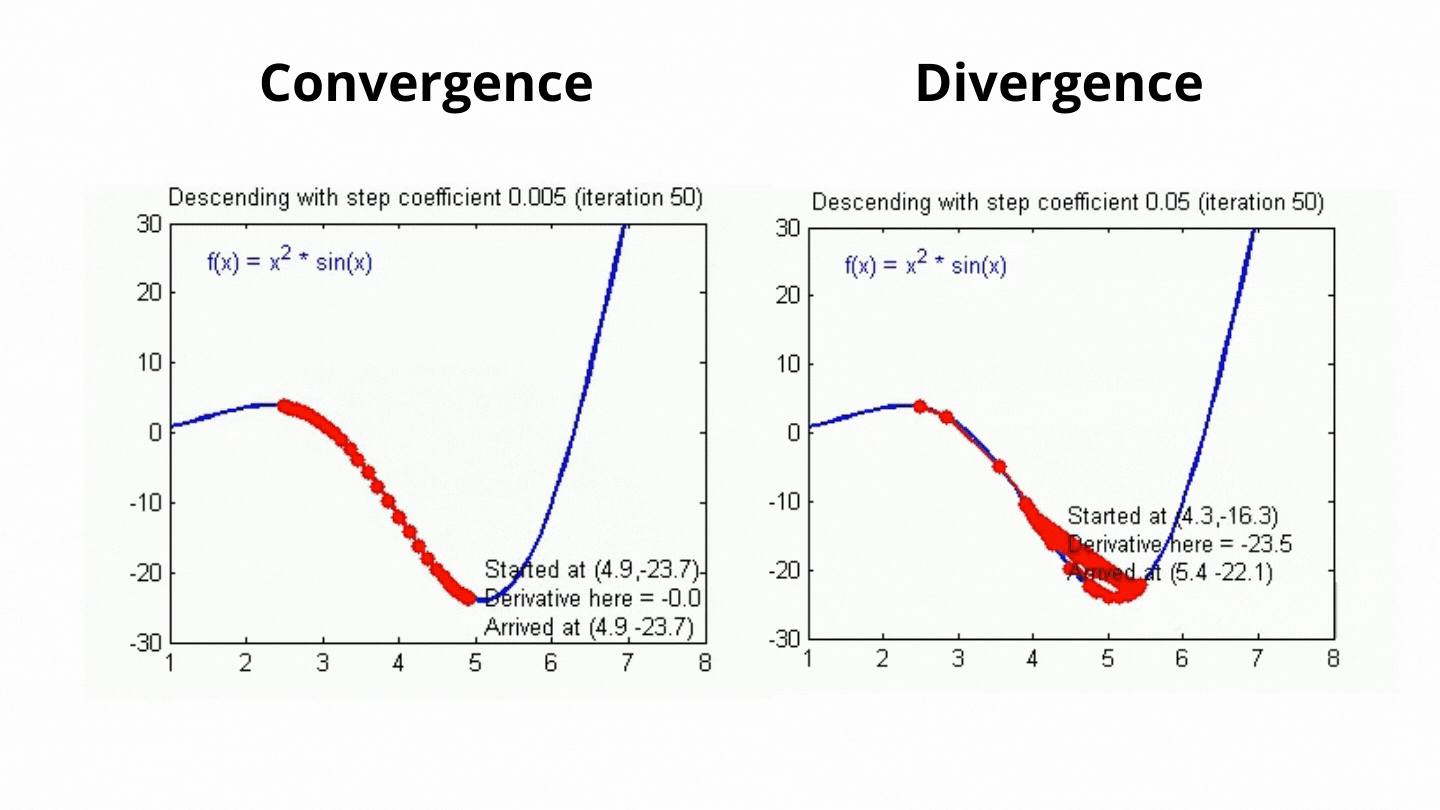
Görüldüğü gibi daha küçük olan öğrenme oranı değerinde minimumu bulma ihtimalimiz artıyorken, büyük öğrenme oranına sahip algoritmada değişimler daha büyük olduğu için minimum hataya ulaşmak daha zor oluyor. Öğrenme katsayısı veriye ve hata fonksiyonuna dikkat edilerek seçilir. Bu katsayı sabit bir değere eşit olabileceği gibi bir fonksiyon şeklinde de tanımlanabilir. Örnek vermek gerekirse algoritma çalıştıkça azalan bir katsayı fonksiyonu belirlenerek algoritma çalıştıkça öğrenme oranı gittikçe azaltılabilir. Veriye uygun katsayıyı bulmaktaki en yaygın yöntem ise deneme yanılma yöntemidir. Belli aralıklarla farklı öğrenme oranı değerleri algoritmaya verilerek algoritmanın hata miktarı gözlemlenir. Bu sayede veri için uygun öğrenme katsayısı bulunabilir.
Sıradaki aşama hata fonksiyonun türevini almak. Bu türev sonucunda ulaştığımız değeri (gradient) öğrenme katsayısıyla çarparız. Minimumu noktayı bulmaya çalıştığımız ve öğrenme katsayısıyla çarparak algoritmanın öğrenme hızını düzenlediğimiz kısım burasıdır. Peki neden türev alıyoruz? Yukarıda grafiklerde de gördüğümüz minimum noktada türev (eğim) sıfır olacaktır. Bunun enlamı nedir? Aşağıya güncelleme denklemimizi yeniden koyalım ve öğrendiğimiz bilgilerle inceleylim.
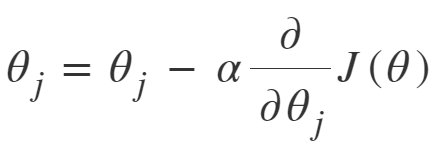
Parametreyi güncellerken;
parmetrenin yeni değeri = parametrenin değeri - öğrenme oranı (a) * fonksiyonun türevi işlemini yapıyoruz. Eğer hata fonksiyonunda minimuma ulaşabilirsek türev sıfıra eşit olacak ve parametrenin değerinden çıkarılan değer de sıfır olacaktır. Bu ne anlama geliyor? Parametrenin eski değeri ile güncel değeri aynı olacak başka bir ifadeyle parametre güncellemesi duracaktır. Bunun sayesinde optimizasyonun sonuna gelmiş olacağız ve algoritma için en iyi parametre değerlerini bulmuş olacağız.
Gradient descent algoritmasının nasıl güncelleme yaptığını bir de örnek üzerinde inceleyelim. Başlangıçta elimizde veriler olsun ve bu verilere en uygun doğruyu (wx + b) bulmaya çalışalım. Hatırlarsanız başlangıçta nöron için wx +b şeklinde bir denkleme ulaşmıştık. Buna benzer bir denklemle işleme devam etmemiz algoritmayı anlamamız açısından avantajımıza olacaktır. Denklemimiz 2x + 5 (Tamamen rastgele belirlendi) olsun. Veriye uygun olup olmadığını bilmiyoruz. Peki ya veriler neler? Verileri temsilen bir tablo oluşturalım.
| X | Y | Tahmin |
|---|---|---|
| 2 | 2 | 9 |
| 4 | 2 | 13 |
| 3 | 3 | 11 |
| 5 | 4 | 15 |
| 6 | 6 | 17 |
Tahmin verisi nedir? Denklemimizden çıkan sonuçtur. Mesela ilk satırda x değeri 2 iken y değeri de 2 dir. Fakat bizim doğrumuz 2x + 5 ile bu değeri temsil etmeye çalıştığımızda 2 * 2 + 5 = 9 değeri ortaya çıkıyor. Başka bir ifadeyle algoritma bu noktanın değerini 9 olarak tahmin ediyor. Ne kadar kötü bir tahmin değil mi? Önce bu verileri grafikte görelim ve doğru parametrelerini optimize etmeye çalışalım.

Verileri temsil etsin diye belirlenen doğrunun parametreleri verileri iyi bir şekilde temsil edemiyor..
Hata metriği olarak MSE (mean squared error) metriğini kullanacağım. Farklı hata metrikleri de burada tercih edilebilir. Parametre güncellerken hata fonksiyonunun türevini alıp bunu öğrenme oranı ile çarpıyorduk.
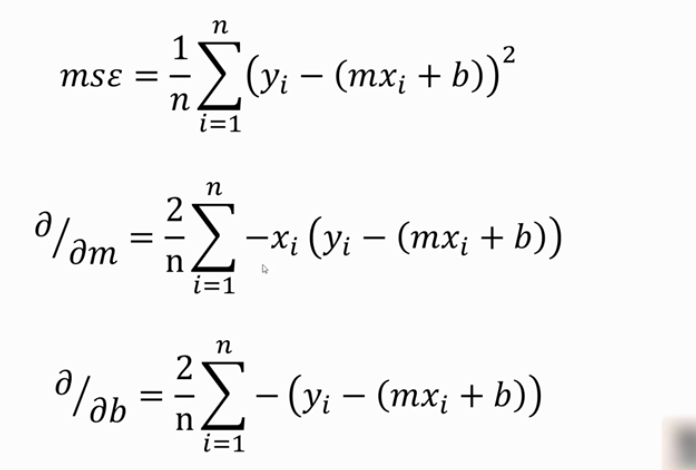
Türevle uğraşmak istemeyen arkadaşlar olabileceği için mse nin türevli hali 2. ve 3. denklemlerdir ve burdaki denklemler direkt kullanılabilir. Peki neden iki denklem çıktı ortaya? Burada dikkat edilmesi gereken bir nokta var. Fonksiyonun türevini güncelleyeceğimiz parametreye göre alıyoruz. Başka bir ifadeyle x in katsayısı güncellenirken ortadaki denklemi, b parametesini güncellerken ise en alttaki denklemi kullanmalıyız. Bu denklemlerdeki y - (mx + b) kısmı gerçek değerlerden tahmin değerlerini çıkardığımız kısımdır. mx + b denklemden çıkan sonuçtur diğer ifadeyle tahmin değerlerimizdir. Bu aşamada bir de öğrenme katsayısına ihtiyacımız olacak. Bu örnek için bu değeri 0.02 kabul edeceğiz.
1. parametre
yeni katsayı = 2 - 0.02 * gradient
gradient ( 2. denklem) = [- 2 * ( 2 - 9) - 4 * (2 -13) - 3 * (3 -11) - 5 * ( 4 -15) - 6 * (6-17)] * (2/5) = 81. 2
yeni katsayı = 2 - 0.02 * 81.2 = 0.376
Çok güzel! x in kasayısının yeni değerini bulduk. Tabii ki denklemi hemen değiştirmiyoruz. Şimdi b parametresini de eski denklemi kullanarak güncelleyeceğiz. İki parametrenin de yeni değerini bulunca denklemin parametrelerini güncelleyeceğiz.
2. parametre
yeni b = 5 - 0.02 * gradient
gradient (son denklem) = [- ( 2 - 9) - (2 -13) - (3 -11) - ( 4 -15) - (6-17)] * (2/5) = 19.2
yeni b = 5 - 0.02 * 19.2 = 4.616
Evet şimdi güncelleme zamanı. Denklemimizin yeni hali 0.376x + 4.616 oldu. Gradient descent algoritması bu doğrunun ilk doğrudan daha iyi olduğunu iddia ediyor. Bakalım gerçekten öyle mi?

Net bir şekilde belli oluyor ki daha iyi parametrelere ve daha az hata miktarına sahip bir denkleme ulaştık. Mükemmel bir denklem mi elde ettik? Tabii ki hayır!. Halen verilere uzağız. Yine de algoritma sadece bir adımda bile bizi verilere gayet güzel bir şekilde yakınlaştırdı ve muhtemelen bir kaç adım sonra veriyi daha iyi temsil eden bir doğru ortaya çıkacaktır. Peki bu kadar işlem sonucunda daha kötü bir doğru elde edebilir miydik? Maalesef evet. Ama bunun en temel sebebi öğrenme katsayısının çok büyük bir değer seçilmesi ve bu sebeple algoritmanın minimum hata noktasını atlamasıdır. Doğru bir öğrenme katsayısıyla algoritma çok güzel çalışacaktır. Algoritmayı detaylı incelemek isteyenler bu gönderiye de göz atabilirler. Genel mantığın anlaşıldığını düşünerek örnek amaçlı daha fazla iterasyon yapmayacağım. Aynı adımlar ulaştığımız yeni denklem için tekrarlanarak optimizasyona devam edilebilir.
Epoch nedir?
Yapay Sinir Ağlarındaki dikkat edilmesi gereken bir diğer nokta epoch kavramıdır. Verinin yapay sinir ağlarında sona kadar gitmesi ve çıktıya göre algoritmanın parametrelerini güncelleyerek başa dönmesinin 1 epoch olduğunu yukarıda yazmıştım. Epoch bir sayıdır ve algoritmanın kendini kaç kere güncelleyeceğini, öğrenme aşamasının kaç kere tekrarlanacağını ifade eder. Bu sayı neden önemlidir? Bu sayı eğer az olursa algoritma veriyi yeteri kadar öğrenemez ve hata miktarı istediğimizden fazla olur. "Peki bu sayının fazla olması ve makinanın veriyi aşırı öğrenmesi neden sorun çıkarsın ki?" diye bir düşünce gelebilir aklımıza. Ama pratikte işler böyle gitmeyecektir. Kurulan model bir yerden sonra veriyi öğrenmeyi bırakıp ezberlemeye başlayacaktır. Başka bir ifadeyle algoritma yorum yeteneğini kaybetmeye başlayacak ve sadece öğrendiği verilerle iyi sonuç verecektir. Yeni veriler geldiğinde bu verileri verimli bir şekilde yorumlayamayacaktır. Epoch sayısı fazla olursa algoritmamız aşağıdaki resimdeki 1. grafik gibi olacaktır. Fakat bizim istediğimiz durum 3. grafiktir. Algoritmanın belli oranda esnek olmasını isteriz.
 Yapay Sinir Ağları detaylı bir şekilde incelenemesi gereken çok fazla nokta barındırsa da genel yapısıyla bu şekildedir. Şimdiden iyi çalışmalar.
Yapay Sinir Ağları detaylı bir şekilde incelenemesi gereken çok fazla nokta barındırsa da genel yapısıyla bu şekildedir. Şimdiden iyi çalışmalar.
Yapay sinir ağları örnek çalışma: Tensorflow ile yapay sinir ağları modeli nasıl kurulur?












Kutay Jan. 25, 2023, 8:11 a.m.
Eline sağlık kardeşim çok açıklayıcı olmuş.
Mustafa Bayhan June 30, 2022, 5:41 p.m.
#DeepLearning