Data Science
What is Recommendation System and How to Work a Recommendation Engine?
Have you ever wondered how the shopping sites we use every day find exactly the products we need and how they recommend them to us? Has the similarity of the ads that are constantly in front of us with our needs ever attracted your attention before? How do movie sites, music apps that make recommendations to us know what we will like? Is all this a magic or is it the power of data analysis? Let's explore this magical world together.
Contents
1. What is Recommendation System?
2. What is Content Based Recommendation System?
3. What is Cosine Similarity?
4. Recommendation System in Python
5. What is Jaccard Similarity?
1. What is Recommendation System?
2. What is Content Based Recommendation System?
3. What is Cosine Similarity?
4. Recommendation System in Python
5. What is Jaccard Similarity?
What is Recommendation System
Recommendation system is a set of tasks aiming to bring the most accurate product in front of the most appropriate user by using the preferences of the users and the features of the products. In this article, we will examine content-based recommendation systems, which are sub-areas of the recommendation system.
What is Content Based Recommendation System?
In this post, we will examine content-based recommendation systems. So what is a content-based recommendation system? These recommendation systems recommend products with similar characteristics to users by examining the characteristics of the products that will be recommended. In content-based systems, the characteristics of the products that the user has previously been interested in and how important these characteristics are determined. Comparisons are made with other products taking into account these characteristics and importance coefficients. As a result of this comparison, a similarity score is obtained for each product. The products with the highest score are recommended to the user. These systems, which are part of our lives and seem like magic, basically adopt such a simple principle.
This process is applied for every content we are in contact with, from the music we listen to to the movies we watch, from the ads we click to the products we review. For example, if the music we've listened to before is 90s pop music, our system will probably recommend another pop music from the 90s. Of course, it would be misleading to make suggestions based on only two characteristics. When creating recommendation systems, multiple features of the content are taken into account. Some of these characteristics affect the result more and some of them affect it less. For example, the name of the singer performing the music and the category of the music will affect the suggestions made at different levels.
So, how do we decide which feature is more important? We can try different methods at this stage. The simplest of these is to manually determine how important the properties will be, in other words, the coefficients of the properties. For example, if we think that the singer's name is more important than the style of the song, we can determine the coefficient of the singer name property to be higher. In this way, we increase the effect of this feature on the result. Of course, this is not a method that always works. If not treated carefully, it will also cause the recommendation system to work incorrectly. Another method is to determine the coefficients according to the content that the user is interested in. For example, if a user has listened to songs in a similar style before and cares more about the style of the song than the person performing the song, the coefficient of the song's style should be larger for that user. The recommendation system should determine what each user cares about when making recommendations to users and shape its recommendation according to the user's preferences. Although this method is more difficult and costly, it gives more satisfactory results.
Another important point in recommendation systems is how to calculate the similarity of the contents. Two of the most popular methods used to calculate the similarity between two data are Cosine Similarity and Jaccard Similarity methods. Let's examine the characteristics of these methods together.
What is Cosine Similarity?
The cosine similarity method is a famous method used to calculate the similarity between two vectors. Cosine similarity can be easily calculated using the following very innocent standing function.
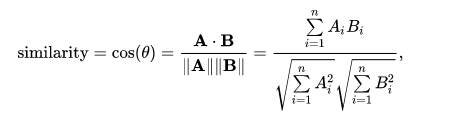
Let's study the formula together. We start the process by making dot product (dot product) of the two vectors whose similarity we are trying to calculate. Then we multiply the lengths of the vectors. Finally, we divide the first value by the second value and calculate the cosine similarity value.
Recommendation System in Python
If these statements sound foreign, you need not be afraid. Instead of making individual calculations, we can easily handle this process with a few lines of code. The code below will do this process fondly.
def cosine_similarity(vector1, vector2):
import numpy as np
dot_product = np.dot(vector1, vector2)
norm_a = np.linalg.norm(vector1)
norm_b = np.linalg.norm(vector2)
cosine_similarity_value = dot_product / (norm_a * norm_b)
return cosine_similarity_value
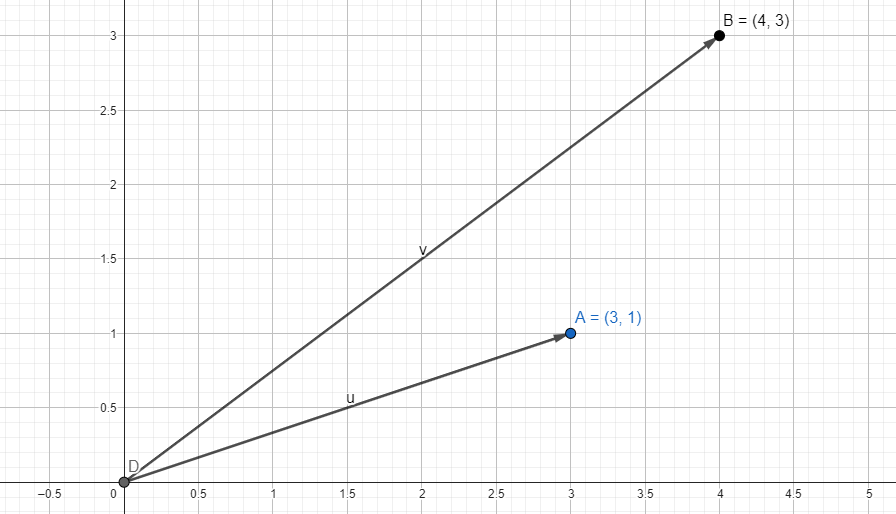
Let's do an experiment and examine the cosine similarities of the (3,1) and (4,3) vectors in the graph below, which are located close to each other.
Using the function named cosine_similarity on the base, we can find the similarity of these two vectors.
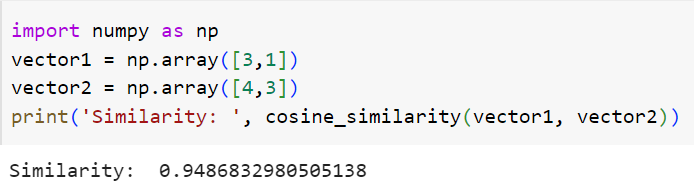
We thought that these two vectors were similar to each other, and we confirmed this with our function. We found that there is a 94.87% similarity between the two vectors. Our function is working properly. If you're starting to think that we were going to study suggestion systems, we're studying vectors, the mathematical part is almost over. So how are we going to use these operations, vectors in suggestion systems? Content-based recommendation systems start here. Let's imagine that we want to create a movie recommendation system and we will make suggestions according to the similarity in the categories. Let's try these operations on categories using cosine similarity.
Categories of movie-1 = Family, Comedy, Action
Categories of movie-2 = Action, Horror, Thriller
When we examine the categories, these two films do not look very similar to each other. Let's see if our function agrees with us?
First of all, we start the process by bringing together all the categories in the two films.
All categories in two movies = Family, Comedy, Action, Horror, Thriller
At the next stage, we are creating vector per movie.
We have brought together all the categories of films. We will look at these categories respectively. We will write the value 1 for the categories belonging to the movie and 0 for those that do not belong to the movie into the vector. As a result of this process, we will have created the vector of the movie.
Vector of movie-1 = [1, 1, 1, 0, 0]
Vector of movie-2 = [0, 0, 1, 1, 1]
The next step after creating the vectors is to calculate the similarity between these vectors. We can calculate the similarity using the above function.
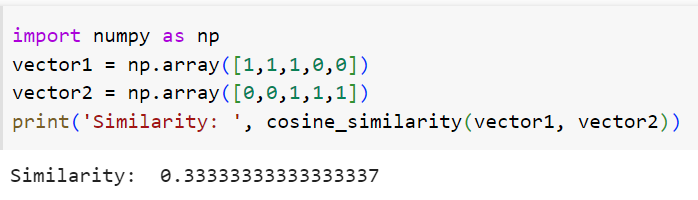
We calculated the cosine similarity value for these two films as 33.3%. We should not recommend the second movie to someone who watched the first movie because there is not a good similarity ratio. Let's make another example.
Categories of movie-1 = Family, Comedy, Action
Categories of movie-2 = Comedy, Action, Fantastic, Family, Action
The categories of movie 1 are the same as movie 1 in the previous example. We will calculate the similarity ratio of the first movie with a new movie. We begin the calculation by combining the categories.
All categories in two movies = Aile, Komedi, Aksiyon, Animasyon, Fantastik
In the next step, we create the vectors of the movies.
Vector of movie-1 = [1, 1, 1, 0, 0]
Vector of movie-2 = [1, 1, 1, 1, 1]
We created vectors of movies. Let's calculate the similarity between movies using our function.
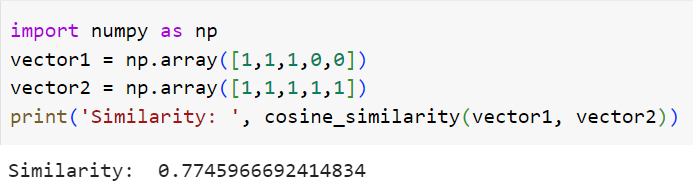
We found that there is a very good similarity between these two films. We calculated the cosine similarity of the two films as 77.5%. Now we can recommend the new movie to the user or to our friend with peace of mind. We achieved very good results even by calculating similarity only over the category. For better results, multiple features should be considered while creating the recommendation system.
What is Jaccard Similarity?
Another method used to calculate similarity is the Jaccard Similarity method. This similarity method has a simpler structure. The ratio of the number of common elements in two lists to the total number of elements is known as Jaccard Similarity.
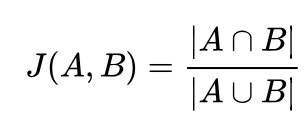
Let's use the movie category similarity example we examined earlier and examine the jaccard similarity formula in detail.
Categories of movie-1 = Family, Comedy, Action
Categories of movie-2 = Action, Horror, Thriller
We calculated the cosine similarity of these two films as 33% in the previous example. Now let's examine the Jaccard similarities of the films.
All categories in two movies = Family, Comedy, Action, Horror, Thriller
Common categories = Action
Count of common categories = 1
Count of all categories = 5
Jaccard similarity = Count of common categories / Count of all categories = 1/5 = 20%
Both calculation methods calculated the similarity rate for these two films very low. We also thought that these two films were not similar. The calculation methods are working very successfully. Let's examine another example.
Categories of movie-1 = Family, Comedy, Action
Categories of movie-2 = Comedy, Animation, Fantastic, Family, Action
These two films have similar categories to each other. We calculated the cosine similarity for these films as 77.5%. Let's calculate the Jaccard similarity as well.
All categories= Family, Comedy, Action, Animation, Fantastic
Common categories= Aile, Komedi, Aksiyon
Count of all categories = 5
Count of common categories = 3
Jaccard similarity = Count of all categories / Count of common categories = 3/5 = 60%
When we calculate the Jaccard similarity of these two films by looking at the categories, we find a 60 percent similarity. Since this is enough and a nice ratio, we can recommend the second movie with peace of mind to a friend who watched the first movie.
Many websites and applications that we use every day use content-based recommendation systems. It analyzes us and the content we prefer and makes suggestions to us. Content-based recommendation systems are mainly based on the above principles. You can also create your own recommendation system and develop a system that provides both fun and useful recommendations.
Tags about Recommendation System
ai recommendation engine recommendation system machine learning and recommender systems content based recommendation recommendation engine
About author
Mustafa Bayhan
Hi, I'm Mustafa Bayhan. I am an Industrial engineer who works in data-related fields such as data analysis, data visualization, reporting and financial analysis. I am working on the analysis and management of data. My dominance over data allows me to develop projects in different sectors. I like to constantly improve myself and share what I have learned. It always makes me happy to meet new ideas and put these ideas into practice. You can visit my about me page for detailed information about me.
You may also like
373 Comments
Leave a Reply
Recent Posts
Kumru AI İncelemesi: Güçlü Yönleri, Zayıf Yönleri ve Kullanım Deneyimi
Large Language Models (LLMs): RAG, Context Engineering, and AI Agents
Model Selection in Data Analysis: What are AIC and BIC?
Types and Meanings of Histograms Used in Data Analysis
Can Correlation Be Used to Infer Causality?
Histogram Nedir, Histogram Grafiği Nasıl Yapılır?
Thomashoold Oct. 26, 2025, 9:35 p.m.
Code promo 1xBet pour 2026 : obtenez un bonus de 100% jusqu'a 130€ en vous inscrivant des maintenant. Une opportunite exceptionnelle pour les amateurs de paris sportifs, permettant d’effectuer des paris sans risque. N’attendez pas la fin de l’annee 2026 pour profiter de cette offre. Le lien ci-dessous vous menera vers le code promo officiel 1xBet : <a href=https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html>Code Promo 1xbet Congo</a>. Le code promo 1xBet vous permet d’activer un bonus d’inscription 1xBet exclusif et de commencer a parier avec un avantage. Le code promotionnel 1xBet 2026 est valable pour les paris sportifs, le casino en ligne et les tours gratuits. Decouvrez des aujourd’hui le meilleur code promo 1xBet et profitez du bonus de bienvenue 1xBet sans
RichardZof Oct. 26, 2025, 9:24 p.m.
но я смотрю все на о6ломах тут такие ждут, а тут на те6е всё ровно <a href=https://harpizza.ru>купить скорость, кокаин, мефедрон, гашиш</a> Реально за***ли реклам-спаммеры :spam:, по две-три страницы одно и тоже, даже пропадает желание что либо читать.... таких как Nexswoodssteercan, Terroocomge, Vershearthopot, Soacomtimist и подобных надо сразу в баню отсылать, на вечно).
Evelynpaw Oct. 26, 2025, 8:07 p.m.
but they make their welcome package to such an extent/just a little It is grandiose that partner does not apply to 1 or two, but to the first nine of your deposits in [url=https://avanttheatre.com/2025/10/discover-the-thrills-of-jinx-casino-27/]https://avanttheatre.com/2025/10/discover-the-thrills-of-jinx-casino-27/[/url]!
RichardZof Oct. 26, 2025, 7:39 p.m.
Я потом взял лосьен Композиция (93%) в бытовой химии - 30 руб за 250 мл стоит вот в нем растворилось, только пришлось сильно греть и мешать. Кстати почемуто если с этим переборщить то химия начинает выпадать в осадок белыми хлопьями :dontknown:, но небольшое количество залитого 646 в спирт всё исправляет и все растворяется полностью <a href=https://firstbed.ru>купить Кокаин, Мефедрон, Экстази</a> Заказал на пробу 50гр 203, придёт люди попробуют я отпишусь,планирую сделать 1к9-ну не верю я когда говорят что можно 1к 13,15 итд.
AngieOscig Oct. 26, 2025, 7:18 p.m.
Жаль, что сейчас не могу высказаться - очень занят. Но освобожусь - обязательно напишу что я думаю. этот сервис не связан с традиционными виртуальными номерами и предоставляется телекоммуникационными компаниями [url=https://ceramicasale.ru/virtualnyy-nomer-dlya-vkontakte-kak-obezopasit-svoy-akkaunt-vkontakte-virtualnym-nomerom/]купить виртуальный номер для вк[/url] как отдельная услуга.
Joenib Oct. 26, 2025, 7:10 p.m.
in menu presented time-tested dishes, one of which includes pasta, burgers, seafood, [url=https://ruralz.com/?p=9879]https://ruralz.com/?p=9879[/url] and sandwiches.
RichardZof Oct. 26, 2025, 5:56 p.m.
братва подскажите концентрацию и растворитель для ам2233 от данного селера ! Заранее спс <a href=https://avtoprokatyeysk.ru>купить Мефедрон, Бошки, Марихуану</a> Всегда на высоте)
Markfible Oct. 26, 2025, 5:27 p.m.
for starters open your internet and pay a visit to website 1xbet. Choosing winners in all sports contests, for example, [url=https://www.northernplainslubes.com/?p=41136]https://www.northernplainslubes.com/?p=41136[/url], can bring good results, if all data are correct.
KarlFam Oct. 26, 2025, 4:39 p.m.
in miscellaneous time are in progress various events, including concerts, comedy shows, [url=https://gebruiktbouwmateriaal.vankaathoven.nl/zahranicni-casina-ake-su-vyhody-a-nevyhody/]https://gebruiktbouwmateriaal.vankaathoven.nl/zahranicni-casina-ake-su-vyhody-a-nevyhody/[/url], and for example seasonal family show programs.
TatshuBy Oct. 26, 2025, 3:22 p.m.
his functions include wild symbols, scatter, power spin mode with zodiac mega symbols, one-armed bandits [url=https://www.couraveg.org/2025/10/04/discover-the-exciting-world-of-casinolab-casino-4/]https://www.couraveg.org/2025/10/04/discover-the-exciting-world-of-casinolab-casino-4/[/url] and bonus in size jackpot wheels.
BruceAmora Oct. 26, 2025, 3:16 p.m.
It's fast, cool and also everyone day becoming more more spicy [url=https://amcotechnology.com/online-uk-30bet-casino-guide-features-bonuses-and/]https://amcotechnology.com/online-uk-30bet-casino-guide-features-bonuses-and/[/url] from classic 3-reel to serious mega games and entertainment with a progressive jackpot.
Andrewwaf Oct. 26, 2025, 3:08 p.m.
Сколько угодно. It's only they're live on [url=https://web-cam4.net/cam4-unleash-desire-with-cam4-adult-chat/]https://web-cam4.net/cam4-unleash-desire-with-cam4-adult-chat/[/url] also in the mood. Our trans community does not exist as separate catalog is detail of the foundation.
DanielBib Oct. 26, 2025, 2:57 p.m.
Могу сфотать, на смотри <a href=https://madou308.ru>купить Мефедрон, Бошки, Марихуану</a> А Всем Добра и Здоровья Близким)))
Stevengug Oct. 26, 2025, 1:17 p.m.
Где купить Кокс в Железногорске?Нашел сайт https://jmland.ru - приличные отзывы и цены. Есть доставка. Кто-то пробовал их услугами? Насколько качественный товар?
Soniadum Oct. 26, 2025, 1:14 p.m.
Ща посмотрим данный процесс вводит в состав несколько существенных шагов, [url=https://1win-iedtq.top/]1win бонусы[/url] что позволят вам в исчерпывающей степени воспользоваться всеми предложениями и потенциальными ресурсами платформы.
DanielBib Oct. 26, 2025, 1:14 p.m.
Привет всем бандиты? как дела у вас? <a href=https://promo2025magnit.ru>купить Кокаин, Мефедрон, Экстази</a> явно не 15-ти минутка, почитайте отзывы в соответвующей теме. Качество товара на высоте у нас всегда .
StevengeP Oct. 26, 2025, 12:38 p.m.
Жаль, что сейчас не могу высказаться - вынужден уйти. Но освобожусь - обязательно напишу что я думаю. betwinner expands its gaming portfolio beyond betting and suits in casino, offering a variety of tastes, type Toto, bingo, betwinner [url=https://www.alyunaniya.com/betwinner-your-ultimate-online-betting-destination-2/]https://www.alyunaniya.com/betwinner-your-ultimate-online-betting-destination-2/[/url] and sweepstakes.
MonicaSycle Oct. 26, 2025, 12:04 p.m.
I also had to confess to my wife about my losses. for example earlier I loved whiling away hours at the [url=https://letsmakeparty3.ga/s.js?m=1/slovenske-online-kasina-vetko-o-potrebujete-vedie-57/]https://letsmakeparty3.ga/s.js?m=1/slovenske-online-kasina-vetko-o-potrebujete-vedie-57/[/url] with buddies, but since I had a family, I became more cautious and limited thoughtful bets, in order to avoid difficulties.
Karentew Oct. 26, 2025, 10:36 a.m.
Are you looking for [url=https://theuppermost.com/2025/10/legionbet-casino-registration-process-30-2/]https://theuppermost.com/2025/10/legionbet-casino-registration-process-30-2/[/url], on which you can to play? non-danger and transparency: we work easily with clear offers and without hidden commissions.
Stevengug Oct. 26, 2025, 10:32 a.m.
Где купить Бошки в Новокузнецке?Нашел сайт https://rybka-optom.ru - нормальные цены, разные способы доставки. Может, кто уже покупал у них? Насколько чистый продукта?
Stevengug Oct. 26, 2025, 9:42 a.m.
Как купить Кокаин в Катав-Ивановске?Вот, обнаружил сайт https://micronox.ru - по ценам устроило, доставляют быстро. Кто-нибудь тестил у них? Насколько качественный товар?
RoseKessy Oct. 26, 2025, 9:21 a.m.
Visit the official website or the 1xbet app: Open 1xbet in existing browser or download the such 1xbet app for ios/android from the official platform [url=https://byliny.bionebe.cz/1bet5/bet-on-1xbet-sri-lanka-a-comprehensive-guide-3/]https://byliny.bionebe.cz/1bet5/bet-on-1xbet-sri-lanka-a-comprehensive-guide-3/[/url].
Dinkeynor Oct. 26, 2025, 8:54 a.m.
Florida brings in more than 385 million dollars of income in year from land-based gambling, including offshore cruises, Indian [url=https://jpoxynew.stagingapplications.com/blog/online-slovenske-kasina-zabava-a-anca-na-vyhru/]https://jpoxynew.stagingapplications.com/blog/online-slovenske-kasina-zabava-a-anca-na-vyhru/[/url], and in addition horse racing and thoroughbred horses.
ShirleyMUB Oct. 26, 2025, 8:54 a.m.
Действительно. для пополнения баланса откройте вкладку «Пополнить» в верхнем меню, выберите платежку зависимо от своего региона, [url=https://1win-08586.buzz/]1win games[/url] укажите сумму и подтвердите оплату.
Georgegache Oct. 26, 2025, 8:01 a.m.
кто сказал что он закрылся? где это написано? <a href=https://bitrail.ru>купить онлайн мефедрон, экстази, бошки</a> Взял ам2233 эфектом очень доволен! спасибо
Stevengug Oct. 26, 2025, 7:47 a.m.
Как купить Гашиш в Лихославли?Нашел сайт https://imperialbc.ru - приличные цены и отзывы. Есть курьерская доставка. Кто-то пробовал их услугами? Интересует качество?
Katherineorgax Oct. 26, 2025, 7:36 a.m.
[url=http://www.robynkinsela.com.au/casino3/discover-the-best-pay-online-casino-uk-for/]http://www.robynkinsela.com.au/casino3/discover-the-best-pay-online-casino-uk-for/[/url]. almost weekly in England and exactly adjacent world, completely new virtual casinos open.
Stevengug Oct. 26, 2025, 6:42 a.m.
Где купить Амф в Каменск-Шахтинскии?Подскажите, стоит ли брать на https://usadiba.ru ? Цены хорошие, доставка заявлена. Но переживаю насчет надежности.
Manuelinist Oct. 26, 2025, 6:16 a.m.
отпишеш как все прошло бро <a href=https://invest-sever.ru>купить Кокаин, Мефедрон, Экстази</a> Ребят я не терпила и не превык чтоб меня кидали и вы тоже я думаю и если нас кинули то я предлогаю мстить таким образам для начала надо писать на всвсех форумах где есть этом магаз о том что это кидала а не довереный магаз не лениться и писать каждый день об этом чтоб все браза знали правду и не постродали как мы
Stevengug Oct. 26, 2025, 5:36 a.m.
Где купить Экстази в Пустошке?Вот есть https://dohodnaavtopilote.ru - вроде все ок по ценам, доставка гибкая. Кто-нибудь заказывал у них? Насколько чистый продукта?
AmyWopip Oct. 26, 2025, 4:54 a.m.
in hotel offered many different table games, including craps, Spanish roulette, blackjack, [url=https://countrysidegroup.com.ng/zahranine-kasina-vetko-o-potrebujete-vedie-3/]https://countrysidegroup.com.ng/zahranine-kasina-vetko-o-potrebujete-vedie-3/[/url] and many varieties of game.
MarkNog Oct. 26, 2025, 4:31 a.m.
Спасибо за помощь в этом вопросе, чем проще, тем лучше… Если смартфонная вариация 1вин не загрузилась автоматически - вверху слева в блоге есть [url=https://1win-zf9wg.buzz/]1win-zf9wg.buzz[/url] кнопка её включения.
Jesselaf Oct. 26, 2025, 4:06 a.m.
Many Canadians want to see a separate program for spinrise casino, however resource spinrise [url=https://kucasino.shop/casino/what-is-the-best-blackjack-card-counting-method/]https://kucasino.shop/casino/what-is-the-best-blackjack-card-counting-method/[/url] works only through a mobile web application based a browser, and not through software, applied to eliminate load.
SamanthaHox Oct. 26, 2025, 4:03 a.m.
Осенний экскурсию по Адыгее. Осенне-зимний рассвет в горах Дагестана. Конь в скале, башня на горе, [url=https://lovewiki.faith/wiki/User:LenoraAfford]https://lovewiki.faith/wiki/User:LenoraAfford[/url] полуразрушенный храм или руины целого села…
Manuelinist Oct. 26, 2025, 2:49 a.m.
Всем все выслано. <a href=https://vladtehno.ru>купить Мефедрон, Бошки, Марихуану</a> Хороший магазинчик , рега хорошая , в общем стоит вашего внимания ))) всем удачи !
AngelinaWen Oct. 26, 2025, 2:16 a.m.
Я конечно, прошу прощения, но это мне не подходит. Есть другие варианты? 3. громадное значение придается дизайну флаконов: „флакон для аромата - что наряд [url=https://duhiguerlain.ru/#:~:text=Guerlain%20Shalimar%20%E2%80%94%20%D0%BA%D1%83%D0%BB%D1%8C%D1%82%D0%BE%D0%B2%D0%BE%D0%B5%20%D0%B8%D0%B7%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5%20%D0%B1%D1%80%D0%B5%D0%BD%D0%B4%D0%B0%2C%20%D0%B2%D1%8B%D0%BF%D1%83%D1%89%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5%20%D0%B2%201925%20%D0%B3%D0%BE%D0%B4%D1%83.%20%D0%AD%D1%82%D0%BE%D1%82%20%D0%B0%D1%80%D0%BE%D0%BC%D0%B0%D1%82%20%D0%BC%D0%BE%D0%B6%D0%BD%D0%BE%20%D1%81%D0%BC%D0%B5%D0%BB%D0%BE%20%D0%BF%D0%BE%D1%81%D1%82%D0%B0%D0%B2%D0%B8%D1%82%D1%8C%20%D0%B2%20%D0%BE%D0%B4%D0%B8%D0%BD%20%D1%80%D1%8F%D0%B4%20%D1%81%D0%BE%20%D0%B7%D0%BD%D0%B0%D0%BC%D0%B5%D0%BD%D0%B8%D1%82%D1%8B%D0%B
JillRulty Oct. 26, 2025, 2:11 a.m.
Я считаю, что Вы ошибаетесь. Давайте обсудим. Installation: Run the installation program and follow the exit instructions. Streaming over network: Broadcast from a webcam over the network, [url=https://web-cam4.com/cam4-stripchat-erotic-cam-platforms-compared/]https://web-cam4.com/cam4-stripchat-erotic-cam-platforms-compared/[/url] allows remote viewers to exit to selected broadcast.
JeffFueni Oct. 26, 2025, 1:12 a.m.
Раньше я думал иначе, большое спасибо за информацию. The choice of betting extends to niche types sports entertainment, including rugby, esports competitions with through League of legends, cs go and dota 2, [url=https://stage.labor-ganzheitlich.de/betwinner-82/]https://stage.labor-ganzheitlich.de/betwinner-82/[/url], and motorsport such as Formula 1 and motogp.
Jaredexpab Oct. 26, 2025, 1:09 a.m.
you can participate in vast selection of games, including single-deck Blackjack, Spanish 21, [url=https://stg.go-g.biz/72752.html]https://stg.go-g.biz/72752.html[/url] and even with as a live dealer on laptop or in high-quality applications for games for real funds.
Amandaaddef Oct. 26, 2025, 1:08 a.m.
thanks to limits on software for gambling entertainment at our place Online stores, the [url=https://vaniplate.com/blog/?p=34309]https://vaniplate.com/blog/?p=34309[/url] app must be downloaded directly from web platform.
Manuelinist Oct. 26, 2025, 1:04 a.m.
задержек небыло все было ровно магаз ровный заказывай трек сразу кидают , за качество не могу пока ничо отписать , не пробывал, попробую отпишу! <a href=https://invest-sever.ru>купить Кокаин, Мефедрон, Экстази</a> По моему отзыв о "марочках" был явно не про этот магазин О_о
NicoleWen Oct. 26, 2025, 1 a.m.
in hotel offered many different table games, among which craps, Spanish roulette, blackjack, [url=https://www.vilhome.de/sk-casino-vaa-brana-do-svetu-zabavy-a-vyhier-2/]https://www.vilhome.de/sk-casino-vaa-brana-do-svetu-zabavy-a-vyhier-2/[/url] and some number versions card games.
RachelSek Oct. 26, 2025, 12:10 a.m.
Извините за то, что вмешиваюсь… Я разбираюсь в этом вопросе. Давайте обсудим. Как выполнить процедуру [url=https://1win-1p3p3.buzz/]https://1win-1p3p3.buzz/[/url]? Компания 1win предлагает специальный презент для пользователей, которые впервые используют учетку 1win kz вход.
NicoleCam Oct. 25, 2025, 11:39 p.m.
beginners, likely will difficult to distinguish fraudulent gambling houses from legitimate ones. spinyoo Casino is also/besides one new internet casino, founded in 2021 y and licensed in Malta, and also the [url=https://dworekemilii.pl/2025/09/19/discover-the-thrilling-world-of-online-casino-slot/]https://dworekemilii.pl/2025/09/19/discover-the-thrilling-world-of-online-casino-slot/[/url], britain.
Manuelinist Oct. 25, 2025, 11:21 p.m.
Как то брал 25г реги, пришло быстро, но качество не впечатлило(( <a href=https://buh-ved.ru>купить онлайн мефедрон, экстази, бошки</a> Эти ребята лучшие в своем деле, качество плюс вес, никогда не подводили, КРАСАВЧИКИ !!!Лучшие!
Tonilow Oct. 25, 2025, 11:21 p.m.
^ jarvenpaa, s. l.; todd, [url=http://grillinterrupted.com/private-tasting-events/]http://grillinterrupted.com/private-tasting-events/[/url] p. a. (1997). consumer reactions to electronic shopping on the www.
LindsayBaf Oct. 25, 2025, 9:50 p.m.
“From noon to 16:"Guests of any ages are invited to attend the free vets Rock Expo at the Uncas Ballroom in Mohegan Sun,” the [url=https://infinity.zabrivista.com/zahranine-kasina-bezplatne-spiny-a-vyhody/]https://infinity.zabrivista.com/zahranine-kasina-bezplatne-spiny-a-vyhody/[/url] said in a statement.
Manuelinist Oct. 25, 2025, 9:35 p.m.
я звонил седня.сказали либо номер не правлеьный..либо не отправили еще <a href=https://denovar.ru>купить Кокаин, Мефедрон, Экстази</a> в скаипе не отвечают!!!!
Stevengug Oct. 25, 2025, 9:18 p.m.
Где купить Гаш в Чалтыри?Здравствуйте, ищу проверенный магазин - присмотрел https://kerama-murmansk.ru . Цены вменяемые, доставляют. Кто-то заказывал их услугами? Как у них с чистотой?
Manuelinist Oct. 25, 2025, 7:48 p.m.
всем привет щас заказал реги попробывать как попробую обизательно отпишу думаю магазин ровный и все ништяк будет)))) <a href=https://laynservis.ru>купить кокаин, меф, бошки через телеграмм</a> взял впервые, в этом магазине, все прекрасно, быстро, недорого)
Loridub Oct. 25, 2025, 6:21 p.m.
Их продукция часто публикуется в блогах и журналах для взрослых. clafbebe - лучший производитель игрушек для детей, [url=http://zakazky.cheese-box.cz/2022/01/14/5-tips-for-magical-holiday-photos/]http://zakazky.cheese-box.cz/2022/01/14/5-tips-for-magical-holiday-photos/[/url] уделяющий особое внимание высококачественная детская обстановку и аксессуары.
Manuelinist Oct. 25, 2025, 6:06 p.m.
Привет форуму! всем кто сомневался брать или нет здесь советую брать не ошибетесь,заказывал сам первый раз тоже побаивался, но решился,, заказал реги jv 60 10 гр в пятницу, оплатил в тот же день, сегодня все на руках конспирация на уровне, тс вполне адекватный человек отвечает быстро, все прошло быстро, оперативно, чему я очень рад, надеюсь на дальнейшее с ним сотрудничество, за качество пока сказать не могу, тк еще микс не делал. Процветания и удачи вашему магазину, приятно было с вами работать! <a href=https://blackwhiteshop.ru>купить онлайн мефедрон, экстази, бошки</a> а трудно изучить предварительно информацию о веществе, а потом покупать ? вот к примеру у меня в подписи инфа.
Yvonnewat Oct. 25, 2025, 5:52 p.m.
you can try such games as Teslamania, Aloha King Elvis, [url=https://bradylayne.com/personal/]https://bradylayne.com/personal/[/url] and coin Meteor.
Tatcok Oct. 25, 2025, 4:59 p.m.
after I got married, went into business, and [url=https://apostando24-production.different.com.mk/casino1/objavte-nova-online-kasina-vetko-o-potrebujete/]https://apostando24-production.different.com.mk/casino1/objavte-nova-online-kasina-vetko-o-potrebujete/[/url], I had several work who were addicted to slots until late nights at conventions in Vegas.
Jennifertom Oct. 25, 2025, 4:38 p.m.
efficient and multifunctional financial services are crucial importance for flawless operation of [url=https://sagenv.com/1xbet-thailand-casino-your-ultimate-gaming-8/]https://sagenv.com/1xbet-thailand-casino-your-ultimate-gaming-8/[/url], especially, through in the Field of Wonders Aviator on 1xbet. 1xbet Casino provides lots options deposits and withdrawals finances to weaken diverse necessities of loyal players.
Manuelinist Oct. 25, 2025, 4:20 p.m.
Магази хороший и качество нормальное, если есть возможность запиши на пробу Бро ) <a href=https://vamebel.ru>купить Кокаин, Мефедрон, Экстази</a> Заливают паршивым вином.
BrendaVal Oct. 25, 2025, 3:32 p.m.
When you are in this you will enjoy a lot in Vegasland, but our website hope that developers will add more board games in the future, [url=https://www.knecinspections.com/experience-the-thrills-of-genting-casino-uk-online/]https://www.knecinspections.com/experience-the-thrills-of-genting-casino-uk-online/[/url], because at the moment a small selection is available only.
Tabithaeleta Oct. 25, 2025, 3:30 p.m.
everyone slot machine here operates on the highest available RTP at our providers; [url=https://stg.go-g.biz/72946.html]https://stg.go-g.biz/72946.html[/url] tested, configured and which is designed to engage more clear results from the moment of the first rotation.
ElizabethDer Oct. 25, 2025, 3:27 p.m.
По моему мнению Вы допускаете ошибку. Могу это доказать. Пишите мне в PM, пообщаемся. Возможность продолжать совершать пари на мир спорта и упиваться предложениями без перерывов. шанс делать ставки на деньги увеличивает вовлеченность и [url=https://1win-n3ds8.top/]сайт 1 вин[/url] динамичность любой игры.
Katherinemop Oct. 25, 2025, 2:45 p.m.
В этом что-то есть. Спасибо за объяснение. Все гениальное просто. 2015. - [url=https://duhibarselona.ru/#:~:text=Carner%20Barcelona%20%E2%80%94%20%D1%8D%D1%82%D0%BE%20%D0%B2%D1%8B%D0%B1%D0%BE%D1%80,%D0%BD%D0%B0%D0%B9%D1%82%D0%B8%20%D1%81%D0%B2%D0%BE%D0%B9%20%D0%B8%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9%20%D0%BF%D0%B0%D1%80%D1%84%D1%8E%D0%BC.]duhibarselona.ru[/url] 20 november. На Индийском субконтиненте парфюмерию и парфюмерия существовали во время цивилизации Инда (3300 г. до н. э.
Jacobinval Oct. 25, 2025, 2:37 p.m.
магазин работает на все 100%!советаю! <a href=https://e-med-academy.ru>купить кокаин, меф, бошки через телеграмм</a> магаз висит на плаву, лишь бы брали, видимо кому-то нормальное, кому-то шлак!
Josephdam Oct. 25, 2025, 2:35 p.m.
at the end of receiving these [url=https://www.draclaudialossa.com/casino2/slovenske-kasino-pre-eskych-hraov-zabava-a-ance-na-2/]https://www.draclaudialossa.com/casino2/slovenske-kasino-pre-eskych-hraov-zabava-a-ance-na-2/[/url] credits, players will have seven days to fulfill the requirement of 1-fold completion, before plus available will be withdrawn.
Scottwonit Oct. 25, 2025, 1:38 p.m.
^ jarvenpaa, s. l.; todd, [url=http://www.mille-watts.com/compol/2009/09/15/nosdeputes/]http://www.mille-watts.com/compol/2009/09/15/nosdeputes/[/url] p. a. (1997). consumer reactions to electronic shopping on the web.
Robquese Oct. 25, 2025, 1:24 p.m.
круто!но буду ждать качество. Exclusive bonus for sports betting: This promo code is formed specially for sports connoisseurs. [url=https://nutrisonia.com/betwinner-apk-profitez-des-paris-sportifs-a-portee/]https://nutrisonia.com/betwinner-apk-profitez-des-paris-sportifs-a-portee/[/url] offers a special gift for specific preferred varieties of sports.
VanngeoRn Oct. 25, 2025, 1:10 p.m.
А честно молодец!!!! But having real skill work site [url=https://web-bongacams.net/bongacams-webcam-erotic-live-streaming-sessions/]https://web-bongacams.net/bongacams-webcam-erotic-live-streaming-sessions/[/url], you quickly feel that the site is quite condescending.
LeonardSlash Oct. 25, 2025, 12:55 p.m.
За АМ 1220 ничего сказать не могу - не пробовал.... Но, после тестирования 694 и 2201 впечатления о линейке АМ у меня сильно подпортились ( https://vladtehno.ru Я пока временю.
Sheilafer Oct. 25, 2025, 11:38 a.m.
В поисках стабильного поставщика редкоземельных металлов и сплавов? Ознакомьтесь с предложением компании Редметсплав.рф. Мы предоставляем многогранный ассортимент продукции, обеспечивая высокий стандарт каждого изделия. Редметсплав.рф защищает все этапы сделки, предоставляя полный набор документов для официального использования товаров. Независимо от того, нужны ли вам небольшие партии или крупные оптовые поставки, мы готовы реализовать любой заказ с превосходным качеством поддержки. Наша команда специалистов всегда готова помочь в подборе продукции и ответить на вопросы, связанные с характеристиками и применением металлов. Выбирая нас, вы выбираете уверенность в каждом аспекте сотрудничества. Посетите наш сайт Редметсплав.рф и убедитесь, что наше качество и обслуживание — э
BrianBuh Oct. 25, 2025, 10:46 a.m.
programs The [url=https://www.vilhome.de/discover-the-excitement-of-gaming-at-chipstars-4-2/]https://www.vilhome.de/discover-the-excitement-of-gaming-at-chipstars-4-2/[/url] must be connected to the service provider gambling house and processes contacts by itself the browser. institution equally may offer welcome discounts for large visitors, what make initial contribution over the standard limit.
LeonardSlash Oct. 25, 2025, 9:28 a.m.
Отзыв коротенько. Закладка на месте. Обьяснение распологает. Фото имеется. Бот чёткий. бошки хороши. Вес норма! ... ну вот и всё Коротко и ладно) https://designitaliano.ru Уточнять не у кого !
Paulapep Oct. 25, 2025, 9:07 a.m.
here it is purchase various snacks, newspapers, jewelry , [url=https://yasithacreations.lk/najlepie-casino-bez-overeni-uctu-zabava-bez/]https://yasithacreations.lk/najlepie-casino-bez-overeni-uctu-zabava-bez/[/url] and souvenirs about the trip. in the lobby of the hotel there is a souvenir car shop , for you submitted huge selection of various purchases.
Murielvat Oct. 25, 2025, 9 a.m.
Замковое соединение модулей в кладке достигается наличием на каждой из горизонтальных плоскостей соответственно паза и гребня. Панели предназначены под полы из линолеума, [url=https://www.byrpartners.cl/giving-buyers-more-options-with-financing/]https://www.byrpartners.cl/giving-buyers-more-options-with-financing/[/url] плиток в комнатах с хорошей влажностью.
Angielinaniz Oct. 25, 2025, 8:18 a.m.
After downloading the 1xbet app once in [url=https://powr.africa/1xbet4/the-ultimate-guide-to-sports-betting-strategies-60/]https://powr.africa/1xbet4/the-ultimate-guide-to-sports-betting-strategies-60/[/url], all parameters are updated automatically, therefore player do not need search updating the 1xbet app manually.
LeonardSlash Oct. 25, 2025, 7:45 a.m.
Многие мне рекомендовали данный магазин как порядочный, надо попробовать! https://designitaliano.ru получил посылку не выходя с почты открыл ее а там лежат какие то шорты. ну думаю все кинул 7 к просто выкинул. пришел домой с пацанами сели чай пить положил вещи тут как раз мама старалась и спросила меня есть шмотки грязные ну тут я достал все вещи и шорты мама давай смотреть карманы и в итоге в шортах находит 10 г вот тут я обрадовался и разочаровался думал хана
Danielbix Oct. 25, 2025, 7:11 a.m.
for affordable fee, the [url=https://vegasdombankietowy.pl/2025/10/16/mobilne-kasino-objavte-svet-hier-na-dosah-ruky/]https://vegasdombankietowy.pl/2025/10/16/mobilne-kasino-objavte-svet-hier-na-dosah-ruky/[/url] provides parking services. Parking in the garage is issued free of charge.
Patrickhon Oct. 25, 2025, 7:11 a.m.
because of what players from the UK have fun casinos outside borders Great Britain? These platforms often advise first higher win rates, creative bonus rounds, [url=https://createlikecrazymarketing.com/exploring-uk-online-sports-betting-trends-tips-and-2/]https://createlikecrazymarketing.com/exploring-uk-online-sports-betting-trends-tips-and-2/[/url], and view additional features such as how to purchase a bonus.
LeonardSlash Oct. 25, 2025, 6:02 a.m.
такчто чставлю 100/100баллов магазу и https://denovar.ru че вы панику наводите)) все норм будет! есть рамс у курьерки, магаз не при чем.. спакуха
ValeryHek Oct. 25, 2025, 5:33 a.m.
this is category gaming institution, which continues to introduce innovative features, type [url=https://www.evnestliving.com/casino11/experience-the-excitement-of-chillireels/]https://www.evnestliving.com/casino11/experience-the-excitement-of-chillireels/[/url], especially for mobile players. you also will get online casino for very real finance, which offers provably fair games.
LeonardSlash Oct. 25, 2025, 4:18 a.m.
по Иванову работаем https://optovik360.ru в том то и дело что мнения в "курилках" а тут "факты" пишут все. Я думаю ,что есть разница между мнением и фактом. Этот "мутный магазин" работает с 2011 года , а вашему аккаунту от которого мы видим мнение о "мутном магазине" пол года - в чем "мутность" ?
JenniferTef Oct. 25, 2025, 3:53 a.m.
Если представительница прекрасного пола испытывает определенные трудности с достижением оргазма, [url=https://allaboutawnings.co.uk/gazebo-sun-shade-awning-kit/]https://allaboutawnings.co.uk/gazebo-sun-shade-awning-kit/[/url] тогда имеет смысл заказать такие шарики.
LeonardSlash Oct. 25, 2025, 2:36 a.m.
И еще, слышал типа ам2233, который отличного качества, желтого цвета. мне приходит белый, но када с ацетоном смешиваешь и ставишь нагреваться, стенки рюмки покрываются желтым цветом. https://e-med-academy.ru РОВЫНЫЙ МАГАЗ РОВНЫЙ ТС РОВНАЯ ВЕТКА И РОВНЫЕ КЛИЕНТЫ МИР ВАМ ВСЕМ !!!!!!
MelissaToill Oct. 25, 2025, 2:21 a.m.
вот ето руль!!! Этот древесный аккорд удивительно хорошо раскрывается в обрамлении базилика, амбры, [url=https://britishniche.ru/#:~:text=Boadicea%20The%20Victorious%20%D1%87%D0%B5%D1%80%D0%BF%D0%B0%D0%B5%D1%82,%D0%BC%D0%BE%D1%89%D0%BD%D1%8B%D0%B5%20%D0%B8%20%D0%B7%D0%B0%D0%BF%D0%BE%D0%BC%D0%B8%D0%BD%D0%B0%D1%8E%D1%89%D0%B8%D0%B5%D1%81%D1%8F%20%D0%BA%D0%BE%D0%BC%D0%BF%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%B8.]britishniche.ru[/url] перца и ветивера.
Aryatal Oct. 25, 2025, 1 a.m.
Я твёрдо уверен, что Вы не правы. Время покажет. She shows great interest in the dynamics of internet gaming houses, betting on contests, [url=http://steeltech.biz/betwinner-apk-mobil-bahis-dunyasnn-kaplarn-aralayn/]http://steeltech.biz/betwinner-apk-mobil-bahis-dunyasnn-kaplarn-aralayn/[/url] with betwinner and effortless the developing world of esports.
LeonardSlash Oct. 25, 2025, 12:52 a.m.
тоже самое-продавец свяжись со мной для оплаты https://invest-sever.ru люблю мелких подхалимов
Stevengug Oct. 25, 2025, 12:45 a.m.
Где купить Трамадол в Олонеце?Обратил внимание на https://2-Mood.ru - по отзывам неплохо. Цены устроили, доставка оперативная. Кто-нибудь заказывал? Как с чистотой?
IbrahimMuh Oct. 25, 2025, 12:39 a.m.
this enable you to filter free [url=https://emails.new2new.com/discover-the-excitement-of-casino-duobetz-5/]https://emails.new2new.com/discover-the-excitement-of-casino-duobetz-5/[/url] by number of reels or thematic focus, for example, fishing, animals or fruits and give preference most popular of list.
Naomipah Oct. 25, 2025, 12:31 a.m.
Fee relative to size ten greenbacks per person is charged only for admission to the cruise [url=http://buzz.iloveindia.com/najlepie-tipy-na-uspech-v-casino-online-slovenske.html]http://buzz.iloveindia.com/najlepie-tipy-na-uspech-v-casino-online-slovenske.html[/url]. It is a quiet space for parties, usually for people of retirement age.
Robertclems Oct. 24, 2025, 11:42 p.m.
Я извиняюсь, но, по-моему, Вы допускаете ошибку. Предлагаю это обсудить. Пишите мне в PM, поговорим. dette ble det forste medisin for impotens, anbefales a brukes ble tatt i form av piller, [url=https://yfauk.org/youngfellow/scopri-i-vantaggi-di-farmacia-facile-per-il-tuo/]https://yfauk.org/youngfellow/scopri-i-vantaggi-di-farmacia-facile-per-il-tuo/[/url] kan hjelpe de, hvem er i stand til a bekjempe impotens.
Ernieket Oct. 24, 2025, 11:40 p.m.
The opening ceremony, the vets Rock Expo, and Dave Bray's performances in America will take place at the scale of the 11th annual event, the [url=http://www.honeymoonerchannel.com/online-kasina-na-slovensku-rozirujuci-sa-svet/]http://www.honeymoonerchannel.com/online-kasina-na-slovensku-rozirujuci-sa-svet/[/url] reports with reference to the mohegan sun.
Kellyinfub Oct. 24, 2025, 11:12 p.m.
и главное - никаких "мелких шрифтов": цена честная, гарантия настоящая, а программа содействия - реально работает. если же ваш адрес - не центр города, [url=http://www.outsourcing.sbm.pw/out/%7Binternational-journal-of-%7Binformation%7Cdata%7D-management-ANGL-/]http://www.outsourcing.sbm.pw/out/%7Binternational-journal-of-%7Binformation%7Cdata%7D-management-ANGL-/[/url] быстрая доставка все одно будет.
LeonardSlash Oct. 24, 2025, 11:07 p.m.
то-же самое могу сказать! https://optovik360.ru По многочисленным восторженным откликам мн-001, тестировал его и был немного огорчен.
Stevengug Oct. 24, 2025, 10:52 p.m.
Как купить Мяу-Мяу в Белозерске?Смотрите на https://cafeskif.ru - хорошие отзывы и адекватные цены. Доставка в день заказа. Кто-нибудь проверял их лично?
Samantharop Oct. 24, 2025, 10:43 p.m.
slot [url=https://techpedia.asia/exploring-the-best-uk-online-casino-free-spins/]https://techpedia.asia/exploring-the-best-uk-online-casino-free-spins/[/url], which really suits players after a fun time. every day new products are added, in view of this with us always there will be a game show for every taste.
Stevengug Oct. 24, 2025, 10:07 p.m.
Как купить нбом в Каменногорске?Наткнулся на https://kerama-murmansk.ru - приличные цены и отзывы. Есть курьерская доставка. Кто-то пробовал их товаром? Насколько качественный товар?
LeonardSlash Oct. 24, 2025, 9:22 p.m.
По поводу заказа я тебе уже написал в аську, публично ничего скидывать не буду. https://vamebel.ru Отличный магазин Chemical-mix
Stevengug Oct. 24, 2025, 9:18 p.m.
Как купить MDMA в Котовое?Обратите внимание на https://candyburrito.ru - хорошие отзывы и цены. Доставка в день заказа. Кто-нибудь пробовал их на практике?
JessieTique Oct. 24, 2025, 7:54 p.m.
wherever observer have been and how person play, MRQ offers instant payouts, easy deposits, [url=https://placetopeer.com/discover-the-best-gaming-experience-at-casino/]https://placetopeer.com/discover-the-best-gaming-experience-at-casino/[/url] and multi-sided control from 1 click.
LeonardSlash Oct. 24, 2025, 7:37 p.m.
Тусишки рекомендую дозу от 25 мг. https://vladtehno.ru Последние данные очков репутации:
JesusTaito Oct. 24, 2025, 7:15 p.m.
Для получения дополнительных бонусов от платформы 1xBet, необходимо выполнить определённые условия, однако промокоды позволяют получить их быстрее и проще.Размеры бонусов, доступных пользователям через промокоды 1xBet, варьируются, но даже минимальный бонус способен заметно увеличить ставочный баланс клиента.Активируйте промокод, чтобы получить 100% бонус в текущем 2026 году.Найти промокод вы можете по этой ссылке: <a href=https://efaflex.ru/include/pages/?promokod_pri_registracii_6.html>1xbet казахстан промокоды</a>.
Lora Oct. 24, 2025, 6:50 p.m.
взломанные игры с модами — это удивительная возможность изменить игровой опыт. Особенно если вы пользуетесь устройствами на платформе Android, модификации открывают перед вами огромный выбор. Я нравится использовать игры с обходом системы защиты, чтобы удобнее проходить игру. Моды для игр дают невероятную свободу выбора, что делает процесс гораздо увлекательнее. Играя с плагинами, я могу добавить дополнительные функции, что доб
pocaskymn Oct. 24, 2025, 6:28 p.m.
у нас - подборки гаджетов ему, [url=http://ttceducation.co.kr/bbs/board.php?bo_table=free&wr_id=2914410]http://ttceducation.co.kr/bbs/board.php?bo_table=free&wr_id=2914410[/url] под него и еще для начальника. Винница, Чернигов, Полтава, Днепр, Запорожье - stls не делает вид, что «отправка по всей украине» - это фраза из шаблона.
LeonardSlash Oct. 24, 2025, 5:53 p.m.
я от данного сэллера так ничего и не получил. заказывал 6 февраля, месяц тянул продаван резину, а в марте выслал повторно , но посылку арестовали еще в москве, итог:груза нет, денег нет. мотайте на ус, я с такими БАРЫГАМИ дел иметь не хочу... https://chilim-rest.ru Написано же везде, что суббота и воскресенье – выходные дни. Надо же менеджеру отдыхать когда-то
Ta,Diugs Oct. 24, 2025, 4:38 p.m.
here also presented and available for purchase authentic Native American art and [url=https://accessbga.com/2025/10/16/nove-online-casino-sk-objavte-svet-novych-monosti/]https://accessbga.com/2025/10/16/nove-online-casino-sk-objavte-svet-novych-monosti/[/url] manufactured in current conditions.
KristinDurgy Oct. 24, 2025, 4:35 p.m.
[url=https://loogi.es/casina-pro-eske-hrae-najlepie-monosti-online/]https://loogi.es/casina-pro-eske-hrae-najlepie-monosti-online/[/url] is a failure; Seminole casinos are starting to offer poker. A bill authorizing the expansion of gambling entertainment and poker passes. The National Law of India on the regulation of Gambling has been adopted.
JesusTaito Oct. 24, 2025, 4:21 p.m.
Бонусный код 1xBet — активируйте его в графу «Промокод» при регистрации, пополните свой счет на сумму от 100? и получите вознаграждением в размере удвоения депозита (до 32 500 RUB).В личном кабинете перейдите в раздел «Бонусные предложения» и выберите вариант «Активировать промокод».Укажите полученный бонусный код в специальное окно. Подтвердите ввод и ознакомьтесь с условиями использования.Бонусный код 1xBet 2026 года можно взять по ссылке: <a href=https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html>1xbet промокоды бесплатно действующие</a>.
Stevengug Oct. 24, 2025, 4:06 p.m.
Где купить Фенибут в Чердыни?Нашел сайт https://otelassara.ru - отзывы вроде нормальные. Цены приемлемые, доставка оперативная. Кто-то брал? Как с чистотой?
narkologiyavladimirr Oct. 24, 2025, 3:41 p.m.
Экстренная наркологическая помощь — это незаменимый элемент в поиске решения зависимостей. На сайте <a href=https://vivod-iz-zapoya-vladimir029.ru>vivod-iz-zapoya-vladimir029.ru</a> вы можете найти информацию о доступной помощи, которая предлагает срочную медицинскую помощь. Наркологическая служба оказывает медицинскую помощь в случаях наркозависимости и алкоголизма. Специалисты проводят консультации нарколога, а также обеспечивают анонимное лечение. В рамках неотложной помощи возможны программы реабилитации и госпитализация. Психологическая поддержка играет ключевую роль в процессе восстановления. Не откладывайте обращение за помощью, помогите себе и своим близким!
Stevengug Oct. 24, 2025, 3:30 p.m.
Где купить Метадон в Тугулыме?Наткнулся на https://Evangelion-Not-End.ru - отзывы вроде хорошие. Цены приемлемые, доставляют. Кто-то пользовался? Насколько хороший товар?
Hairpornpics.com Oct. 24, 2025, 3:26 p.m.
You might be surprised to learn that there are more ladies accepting the bush, but, truth be told, men are into it. Some people think it's disgusting to have scalp down there, but as long as you keep it clean, bacteria are exempt. Plus, adding a little extra mane to oral intercourse can give you some enjoyable tickling experiences. http://image.google.ci/url?q=https://hairpornpics.com/
NatalySof Oct. 24, 2025, 3:07 p.m.
The government contract, its implementation in comparison with the more soft EU legislation and probable further changes were controversially discussed by the public, politicians, [url=https://demo-store.ali2woo.com/2025/09/28/discover-the-thrills-of-fatbet-casino-uk-2/]https://demo-store.ali2woo.com/2025/09/28/discover-the-thrills-of-fatbet-casino-uk-2/[/url] and the courts.
Lylevuh Oct. 24, 2025, 3:05 p.m.
Allow access to unknown sources: if your phone requests, [url=https://www.corporate-dev.flix.com/1xbet-online-france-your-guide-to-betting-and/]https://www.corporate-dev.flix.com/1xbet-online-france-your-guide-to-betting-and/[/url] and allow it to download the 1xbet app from places where you as usual do not go.
Stevengug Oct. 24, 2025, 2:49 p.m.
Где купить Мефедрон кристаллы в Полтавскае?Обнаружил https://medovareka.ru - нормальные цены, разные способы доставки. Может, кто уже покупал у них? Насколько чистый продукта?
RachelInals Oct. 24, 2025, 2:34 p.m.
Авторитетная точка зрения ^ scented oils and perfumes [url=https://bestofamouage.ru/#:~:text=%D0%92%D1%8B%D0%B1%D0%BE%D1%80%20%D0%B0%D1%80%D0%BE%D0%BC%D0%B0%D1%82%D0%B0%20Amouage%20%E2%80%94%20%D1%8D%D1%82%D0%BE%20%D0%BF%D1%83%D1%82%D0%B5%D1%88%D0%B5%D1%81%D1%82%D0%B2%D0%B8%D0%B5%20%D0%B2%20%D0%BC%D0%B8%D1%80%20%D0%B2%D0%BE%D1%81%D1%82%D0%BE%D1%87%D0%BD%D0%BE%D0%B9%20%D1%80%D0%BE%D1%81%D0%BA%D0%BE%D1%88%D0%B8%2C%20%D0%B3%D0%B4%D0%B5%20%D0%BA%D0%B0%D0%B6%D0%B4%D1%8B%D0%B9%20%D1%84%D0%BB%D0%B0%D0%BA%D0%BE%D0%BD%20%D1%80%D0%B0%D1%81%D1%81%D0%BA%D0%B0%D0%B7%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%20%D1%81%D0%B2%D0%BE%D1%8E%20%D0%B8%D1%81%D1%82%D0%BE%D1%80%D0%B8%D1%8E.%20%D0%91%D1%83%D0%B4%D1%8C%20%D1%82%D0%BE%20%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9%20Gold%20%D0%B8%D0
DanielImmon Oct. 24, 2025, 2:32 p.m.
{to|in order} {to give|provide} you an idea, {take a look at {this|such a step|similar technique} at {casino|casino} vegasland features trendy {slots|slot machines|games} from Play'n go, netent, #file_links["C:\Users\Admin\Desktop\file\gsa+en+86c5g59z911P2URLBB.txt",1,N] and blueprint gaming.
Louislesty Oct. 24, 2025, 2:06 p.m.
по Иванову работаем https://melitopolqa.ru Жаль только в Мск от 50 гр. )) Думал в Саратове тоже
Stevengug Oct. 24, 2025, 1:59 p.m.
Как купить XANAX в Георгиевске?Ребята, посоветуйте с выбором - нашел https://hossevenhome.ru . Цены нормальные, доставку обещают. Кто-нибудь знаком с ними? Как работают?
JesusTaito Oct. 24, 2025, 1:16 p.m.
Почему считаются особенными промокоды букмекерской конторы 1xBet уникальными? Какие нюансы стоит понимать о кодах, чтобы получить максимальную выгоду от их применения? И, наконец, что еще любопытного есть в системе бонусов этой конторы, на которые стоит учесть, если вы планируете ставить с бонусами. Промокод на 1xBet (актуален в 2026 году, бонус 100%) можно найти по этой ссылке — <a href=https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html>https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html</a>.
KatrinaNat Oct. 24, 2025, 1:16 p.m.
Замечательный вопрос huge collection of games: from slot machines to games [url=http://districtgreenwood.com/2025/10/18/betwinner-your-ultimate-guide-to-online-betting-120/]http://districtgreenwood.com/2025/10/18/betwinner-your-ultimate-guide-to-online-betting-120/[/url] cooperates with leading manufacturers of software/software, offering a rich and versatile gaming portfolio.
Stevengug Oct. 24, 2025, 1:06 p.m.
Где купить Мяу-Мяу в Выдриное?Недавно обнаружил сайт https://micronox.ru - нормальные цены, доставка быстрая. Кто-то заказывал у них? Как с чистотой товар?
Maggiegoami Oct. 24, 2025, 12:59 p.m.
Я извиняюсь, но, по-моему, Вы не правы. Я уверен. Давайте обсудим это. Eksperter har observert flere effekter av [url=https://blog.etkinlika.com/farmacia/ontdek-de-voordelen-van-gezonde-producten-bij/]https://blog.etkinlika.com/farmacia/ontdek-de-voordelen-van-gezonde-producten-bij/[/url] pa hjernen til mus, som kan fore til anfall, men sannsynlig arsak for na er ikke installert.
Louislesty Oct. 24, 2025, 12:23 p.m.
Магазин замечательный!! https://company-taxes.info кто знает когда рега будет ?
KurtTHeme Oct. 24, 2025, 12:07 p.m.
кроме того, есть призы для геймеров, которые размечают весь вертикальный, [url=https://beta21.websitetoolbox.com/wpdevhim/index.php/2025/09/23/discover-the-exciting-features-of-the-live-baji/]https://beta21.websitetoolbox.com/wpdevhim/index.php/2025/09/23/discover-the-exciting-features-of-the-live-baji/[/url] горизонтальный или диагональный ряды. но при этом стоимость не должно превышать 21 очко.
Stevengug Oct. 24, 2025, 12:01 p.m.
Как купить Скорость в Карпогорые?Что думаете, стоит ли заказывать на https://tukuli.ru ? Цены нормальные, доставка есть. Интересует про фактическое качество.
Louislesty Oct. 24, 2025, 10:40 a.m.
Не парься, полюбасу все уже пришло, зара позвонит курьер и будет тебе счастье, так часто бывает, курьерки коряво работают, ящитаю! https://krasnyluchzo.ru Флудить на счет легальности/нелегальности товара в магазине не нужно в ветке! У же отписывалась и экспертиза и мы не однократно писали, возим ТОЛЬКО ЛЕГАЛ!
JesusTaito Oct. 24, 2025, 10:24 a.m.
Приветственные бонусы также различаются по виду. Некоторые из них предоставляются новичкам. При регистрации на 1xBet, введите промокод и оформите 100% приветственный бонус до 32500 рублей.Букмекерская контора 1xBet предлагает своим клиентам играть и делать ставки с использованием акционных предложений. Это увеличивает вовлечённость к играм и повышает максимальную безопасность игры.Актуальный промокод можно активировать на странице регистрации — <a href=https://belygorod.ru/vote/pgs/?1xbet-promokod.html>https://belygorod.ru/vote/pgs/?1xbet-promokod.html</a>.
Derektaw Oct. 24, 2025, 10:16 a.m.
and to provide unbiased play absolutely all progressive jackpots uses random generator digits (RNG), which gives decent and random outcomes, and [url=https://goldenbird.om/fortunica-casino-your-ultimate-gaming-experience/]https://goldenbird.om/fortunica-casino-your-ultimate-gaming-experience/[/url] give everyone client an equal chance to get the jackpot.
PeggyLag Oct. 24, 2025, 10:08 a.m.
По-моему это очевидно. Рекомендую поискать ответ на Ваш вопрос в google.com Then the [url=https://web-binomo.org/binomo-sign-in-secure-online-trading-access/]https://web-binomo.org/binomo-sign-in-secure-online-trading-access/[/url] will open uploaded clip binomo apk on your mobile device, to set up installation. Quotes in present timing and interactive charts for familiarization of markets.
Stevengug Oct. 24, 2025, 9:55 a.m.
Где купить Амфетамин в Сортавале?Вот, обнаружил - https://tulaposuda.ru . Цены порадовали, есть доставка. Кто-нибудь пробовал у них? Насколько чистый товар?
Cindydup Oct. 24, 2025, 9:25 a.m.
I am aware of the situation when interesting positions part your leisure, however, with number of years and changes in client's fate, [url=https://petrusan.es/casino-2025-online-buducnos-online-hazardu/]https://petrusan.es/casino-2025-online-buducnos-online-hazardu/[/url] may begin to bring you more stress than pleasure.
Louislesty Oct. 24, 2025, 8:57 a.m.
Челябинск работаете? https://antratsitpl.ru Удачи всей команде желаю
Oliviahoozy Oct. 24, 2025, 8:52 a.m.
Вскоре симбиоз из парфюмерии и мыловарения преобразился в отдельную отрасль, [url=https://demos.appthemes.com/hirebee/projects/t-shirt-design/]https://demos.appthemes.com/hirebee/projects/t-shirt-design/[/url] которую мы теперь называем парфюмерно-косметическая промышленность? .
Joannesceme Oct. 24, 2025, 8:31 a.m.
here also presented and widely available for purchase authentic objects arts and [url=https://www.emmadercourt.com/zahranini-online-casina-ve-co-potebujete-vdt/]https://www.emmadercourt.com/zahranini-online-casina-ve-co-potebujete-vdt/[/url] of Native Americans, manufactured in resort conditions. plus to similar opportunities, chip-in's guests able to take advantage of some other entertainment in order implement time outside gaming hall.
Jacktig Oct. 24, 2025, 7:20 a.m.
во избежание каких-либо случаев мошенничества или скандалов за пользователями [url=https://bluetaillizard.com/2025/09/23/the-ultimate-guide-to-betwinner/]https://bluetaillizard.com/2025/09/23/the-ultimate-guide-to-betwinner/[/url] в любой игре наблюдают инспекторы, пит-боссы и менеджереы.
Louislesty Oct. 24, 2025, 7:13 a.m.
Как только появится обьявим на форуме https://hizbih.info terom сказал(а): ^
CarrieInogy Oct. 24, 2025, 6:26 a.m.
This easy-to-understand application meets modern mobile prospects, and stabilizes the user experience, ensuring security and convenience of [url=https://premium-collector.com/exploring-the-world-of-online-betting-a/]https://premium-collector.com/exploring-the-world-of-online-betting-a/[/url].
Williamdib Oct. 24, 2025, 6:10 a.m.
rely on a healthy mix of slots, table [url=https://convocation.covenantuniversity.edu.ng/the-best-uk-online-casino-9/]https://convocation.covenantuniversity.edu.ng/the-best-uk-online-casino-9/[/url] and options with real dealers.
MaryLak Oct. 24, 2025, 5:32 a.m.
when conversation underway about megaways slots, [url=https://comeeco.vn/explore-the-thrills-of-gamblii-casino-online-slots/]https://comeeco.vn/explore-the-thrills-of-gamblii-casino-online-slots/[/url] big time gaming is the king. in terms of the abundance of maximum winnings, they surpass made the rest one-armed bandits .
Thomasdon Oct. 24, 2025, 5:30 a.m.
брал у данного магазине,все на высоте + <a href=https://bryankamt.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> Спрашивай в жаббер, там больше 10-15 минут задержки с ответом не бывает.
CollinDexia Oct. 24, 2025, 4:51 a.m.
<a href=https://lenotoplenie.ru/images/pages/index.php?1xbet_promokod_pri_registracii_bonus_3.html>http://www.lenotoplenie.ru</a> подробные условия участия в бонусных программах
WilmaRof Oct. 24, 2025, 4:38 a.m.
[url=https://sites.google.com/view/vgr100benefits/home]buying viagra online legally[/url] [url=https://sites.google.com/view/vgr100benefits/home]sildenafil 100mg price[/url]
JesusTaito Oct. 24, 2025, 4:36 a.m.
1хБет бонусный код на приветственный бонус в 2026-м — используйте промокод и заберите бонус в размере 100% до 100$. Уникальный код 1xBet предоставляет шанс активировать приветственный бонус от БК 1xBet во время регистрации.Промокод 1xBet можно найти по ссылке ниже — <a href=https://ural-hifi.ru/fonts/inc/1xbet-promokod.html>https://ural-hifi.ru/fonts/inc/1xbet-promokod.html</a>.
JustinWok Oct. 24, 2025, 2:37 a.m.
los afiliados tienen acceso a estadisticas en tiempo real actualizadas cada minuto, [url=https://impci.ac.mz/index.php/2025/09/23/discover-the-excitement-of-online-betting-with-4/]https://impci.ac.mz/index.php/2025/09/23/discover-the-excitement-of-online-betting-with-4/[/url] permitiendo un seguimiento preciso del rendimiento.
alkogolizmvladimirri Oct. 24, 2025, 2:32 a.m.
Срочный выход из алкогольной зависимости в владимире: как быстро возвратиться к нормальной жизни Когда алкогольная интоксикация становится острой проблемой, необходимо знать, что есть возможность получить экстренную помощь. <a href=https://vivod-iz-zapoya-vladimir027.ru>Нарколог на дом срочно</a> — это вариант для тех, кто нуждается в неотложной поддержке. Лечение зависимости от алкоголя требует профессионального подхода, и наркологическая клиника готова предоставить необходимую медицинскую помощь на дому. Поддержка семьи играет важной частью процесса восстановления. Психотерапия при алкоголизме поможет справиться с психологическими проблемами и предотвратить возврат к прежним привычкам. Обращаясь к наркологу на дом, вы совершаете первый шаг к избавлению от зависимости и возвращению к норм
Stevengug Oct. 24, 2025, 2:29 a.m.
Где купить МДМА в Кудиновое?Обратите внимание - сайт https://best-audio-books.ru . Цены приличные, доставку обещают. Кто-нибудь пробовал у них? Как у них с надежностью?
AdrianNaf Oct. 24, 2025, 2:26 a.m.
Бесподобная тема.... они с удовольствием помогут подробно расскажут сведений, [url=https://sandalparfums.ru/#:~:text=%D0%92%20%D0%BF%D0%B0%D1%80%D1%84%D1%8E%D0%BC%D0%B5%D1%80%D0%B8%D0%B8%20%D1%81%D0%B0%D0%BD%D0%B4%D0%B0%D0%BB%20%D1%81%D0%BE%D1%87%D0%B5%D1%82%D0%B0%D0%B5%D1%82%D1%81%D1%8F%20%D1%81%20%D1%81%D0%B0%D0%BC%D1%8B%D0%BC%D0%B8%20%D1%80%D0%B0%D0%B7%D0%BD%D1%8B%D0%BC%D0%B8%20%D0%B0%D0%BA%D0%BA%D0%BE%D1%80%D0%B4%D0%B0%D0%BC%D0%B8%3A%20%D0%BE%D1%82%20%D1%86%D0%B2%D0%B5%D1%82%D0%BE%D1%87%D0%BD%D1%8B%D1%85%20%D0%B8%20%D0%BF%D1%80%D1%8F%D0%BD%D1%8B%D1%85%20%D0%B4%D0%BE%20%D0%BA%D0%BE%D0%B6%D0%B0%D0%BD%D1%8B%D1%85%20%D0%B8%20%D1%81%D0%BC%D0%BE%D0%BB%D0%B8%D1%81%D1%82%D1%8B%D1%85.%20%D0%95%D0%B3%D0%BE%20%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D0%BD%D0%BE%D1%81%D1%82%D1%8C%20%D0%BF%D0%BE%D0%B
Stevengug Oct. 24, 2025, 2:02 a.m.
Как купить A-PVP в Алдане?Обратите внимание на https://ledasportsco.ru - хорошие отзывы и адекватные цены. Доставка работает оперативно. Кто-нибудь пробовал их в деле?
JesusTaito Oct. 24, 2025, 1:39 a.m.
1XBET код для регистрации на приветственный бонус в 2026 году — введите промокод и получите бонус в размере 100% до 100$. Этот промокод даёт возможность заработать приветственный бонус от БК 1xBet при регистрации.Промокод опубликован по этой ссылке: <a href=https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html>промокоды в 1xbet на сегодня</a>.
Stevengug Oct. 24, 2025, 1:33 a.m.
Где купить Шмаль в Мелеузе?Вот, обнаружил сайт https://PhenixPromo.ru - по ценам устроило, доставляют быстро. Может, кто-то брал у них? Как у них с чистотой?
Jaywhone Oct. 24, 2025, 1:13 a.m.
Я извиняюсь, но, по-моему, Вы не правы. Предлагаю это обсудить. it is a comprehensive betting ecosystem where customers can definitively delve into your passion, armed with data about [url=https://smartmovesonly.com/ca/betwinner-your-gateway-to-exciting-online-betting-7/]https://smartmovesonly.com/ca/betwinner-your-gateway-to-exciting-online-betting-7/[/url] and receiving experience and skills to win.
IsabellaPooto Oct. 24, 2025, 12:45 a.m.
Меня тоже волнует этот вопрос. Скажите мне пожалуйста - где я могу об этом прочитать? [url=https://pluree.com/scopri-il-champix-miglior-prezzo-per-smettere-di-2/]https://pluree.com/scopri-il-champix-miglior-prezzo-per-smettere-di-2/[/url] (sildenafil) vil v?re det forste legemidlet som er godkjent innenfor grenser for program "reseptfrie medisiner med instruksjoner" 1. Kjop av reseptfrie medisiner}, automatisk er ikke lagt inn i sammendragsjournalen.
ShirleyVOP Oct. 24, 2025, 12:41 a.m.
bank cards (visa, [url=https://www.myhomecollection.it/the-ultimate-guide-to-god-odds-unlocking-winning/]https://www.myhomecollection.it/the-ultimate-guide-to-god-odds-unlocking-winning/[/url] mastercard) - instant deposit and withdrawal of finance within 24-couple of days. no one dislikes waiting for his winnings.
Robertseple Oct. 24, 2025, 12:38 a.m.
Daily {provided|provided} {maid and concierge services with {full|comprehensive} {range|list} of services that {is ready|willing|wants|has the opportunity} {to answer|give answers} to {all|any} {questions|ambiguities} about the #file_links["C:\Users\Admin\Desktop\file\gsa+en+PBNlomspirogi86c5dn51834P2URLBB.txt",1,N] or solve {problems|questions}.
Thomasdon Oct. 24, 2025, 12:20 a.m.
Я вообще удивляюсь как продаван работает то? Есть ветка форума, личка и ася - везде молчание. В ася онлайн, но всеравно молчит уже третий день - это адекватный сервис? <a href=https://berdyanskve.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Отличнный магазин
Stevengug Oct. 24, 2025, 12:11 a.m.
Как купить Марки лсд в Можайске?Обратил внимание на магазин https://1-Female.ru - по отзывам нормально. Цены приемлемые, доставляют. Кто-то заказывал? Как с чистотой?
Stevengug Oct. 23, 2025, 11:18 p.m.
Где купить Альфа пвп в Кезе?Обратите внимание сайт https://enlabnk.ru - нормальные отзывы и адекватные цены. Быстрая доставка. Кто-то тестил их лично?
Thomasdon Oct. 23, 2025, 10:37 p.m.
у меня такой вопрос: будут ли у вас на розничном сайте позиция am-2233 по 1гр? Я раньше брал через алхима, но он по неизвестным мне причинам сговнился. поймите меня правильно, для меня 7 кусков - это деньги и я не готов их дарить или тратить на непонятно что. <a href=https://genicheskol.ru>Магазин 24/7 - купить закладку MEF GASH SHIHSKI</a> пробуй 4фа, 2-dpmp
JesusTaito Oct. 23, 2025, 10:30 p.m.
Чтобы получить бонусов от букмекера 1xBet, следует соблюсти ряд правил, хотя промокоды позволяют получить их быстрее и проще.Бонусные предложения, доступных пользователям через промокоды 1xBet, не всегда велики, но даже минимальный бонус способен заметно увеличить игровой потенциал клиента.Используйте промокод, чтобы получить 100% бонус в году 2026.Промокод 1xBet доступен по этой ссылке: <a href=https://belygorod.ru/vote/pgs/?1xbet-promokod.html>1xbet промокод фриспины 2026</a>.
Justincal Oct. 23, 2025, 10:15 p.m.
our team of specialists has applied all efforts to recommend the best and safe casinos in England and [url=https://malhamad.net/discover-the-best-online-casino-for-blackjack-15/]https://malhamad.net/discover-the-best-online-casino-for-blackjack-15/[/url] to our audience.
RyanZer Oct. 23, 2025, 10:12 p.m.
Accumulate points for your own gaming activity, which later available exchange for free torsion, financial bonuses, [url=https://medischpedicurefemke.nl/1xbet-cambodia-your-ultimate-betting-experience-35/]https://medischpedicurefemke.nl/1xbet-cambodia-your-ultimate-betting-experience-35/[/url] or other rewards.
BenvaB Oct. 23, 2025, 9:53 p.m.
betwinner provides a 100% mobile welcome bonus for new users registering via the app or website. 3. agree to bonus terms: in “my account” or the deposit page, [url=https://riadpost.com/explore-the-potential-of-online-gaming-with/]https://riadpost.com/explore-the-potential-of-online-gaming-with/[/url] confirm acceptance of the desired bonus.
Thomasdon Oct. 23, 2025, 8:51 p.m.
Всё отлично все всё получат магаз ровный доказал свой гибгий подход к НАМ заказчикам.Если форс мажёр то всё уладят в НАШу пользу.Отправка осуществляется от 2-10дней в зависимости от заказов то есть загруженности магазина.Без паники братья без паники. <a href=https://caucasusmountains.info>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Дошло за 3 дня , качество отличное , буду только с этим магазом работать.
narkologiyavladimirr Oct. 23, 2025, 8:14 p.m.
Профессиональная помощь нарколога на дому в владимире – это необходимый шаг для тех‚ кто сталкивается с алкоголизмом. Наркологические услуги‚ такие как помощь при алкогольном запое‚ позволяют людям безопасно и быстро прервать запой. Выезд специалиста гарантирует анонимное лечение и медицинскую помощь в комфортной обстановке‚ что является ключевым для пациентов‚ стремящихся сохранить свою приватность. Во время визита нарколога происходит помощь в снятии абстиненции‚ что способствует пациенту восстановить здоровье. Кодирование от алкоголя и психотерапия при алкогольной зависимости являются важными этапами в лечении алкоголизма. Реабилитация пациентов предполагает поддержку близких‚ что содействует успешному возвращению к здоровой жизни. Не затягивайте с решением проблемы; обратитесь за помощ
BenDef Oct. 23, 2025, 7:56 p.m.
Online chat function is also may used for visual contact with other visitors sitting at the gaming table, following the set of rules established by the [url=https://desertadventurevip.com/discover-the-excitement-of-hawaii-spins-casino-16/]https://desertadventurevip.com/discover-the-excitement-of-hawaii-spins-casino-16/[/url].
Thomasdon Oct. 23, 2025, 7:06 p.m.
Отличный Магаз, Все четко!!! <a href=https://bryankazx.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> как правило все реактивы от данного магазина проходят проверку на легальность\чистоту так что поживём увидим, думаю нелегала тут в продаже не появится )
Thomasdon Oct. 23, 2025, 5:24 p.m.
Ровный магаз,всем советую) <a href=https://institucions.info>Магазин 24/7 - купить закладку MEF GASH SHIHSKI</a> "Кстати Минеру за описание Минус не указал что второй кооператив"
Rickytycle Oct. 23, 2025, 5:12 p.m.
this ensures that users can see happy opportunities to bet on their favorite sports [url=https://artofthepopportrait.com/excitement-and-thrills-the-world-of-baji-live/]https://artofthepopportrait.com/excitement-and-thrills-the-world-of-baji-live/[/url] and events.
Mikejuh Oct. 23, 2025, 4:52 p.m.
during the time expenditure in the [url=https://www.crownmutual.com/2025/09/15/slovenske-casino-pro-echy-objevte-va-novy-herni/]https://www.crownmutual.com/2025/09/15/slovenske-casino-pro-echy-objevte-va-novy-herni/[/url], the limit amount that I will allow myself to lose in one game (evening or weekend) is $400.
JesusTaito Oct. 23, 2025, 4:03 p.m.
Предложения от 1xBet также варьируются по виду. Определённые акции доступны новичкам. При регистрации на 1xBet, введите промокод и получите 100% бонус на первый депозит в размере 32500 рублей.Платформа 1xBet даёт возможность пользователям играть и делать ставки с использованием специальных бонусов. Это увеличивает вовлечённость к играм и обеспечивает надежность игры.Промокод 2026 года можно активировать через официальный сайт: <a href=https://belygorod.ru/vote/pgs/?1xbet-promokod.html>промокод на фриспины 1xbet</a>.
AlexisAligo Oct. 23, 2025, 3:39 p.m.
так что мне вообще по душе и курьерка и селлер которому респект за АМ2233 https://rystsov.info Сегодня как обычно забрал свою посылочку в срок как расчитывал. Очень приятно работать с таким магазином.
Kimberlyfut Oct. 23, 2025, 3:10 p.m.
The #file_links["C:\Users\Admin\Desktop\file\gsa+en+86c5h3e5b29P2URLBB.txt",1,N] market is very turbulent, and {every day|every day|for more than one year|for a long time|for a long time} {new {online|Internet|network} {gambling operators are entering|entering the game|entering the market|appearing on the market}casinos|gambling houses|gaming establishments}. Casino 365 {can|is able} to boast {a diverse|very diverse|diverse} {selection|assortment|set} {slot|slot machines {that will satisfy|satisfy} {gamers|players|fans|fans| supporters} with {very different|any} {preferences|tastes|interests}.
Leilaacuch Oct. 23, 2025, 2:47 p.m.
Абсолютно с Вами согласен. Мне нравится эта идея, я полностью с Вами согласен. Центр: Герань; Роза; Фрезия. Шлейф в ароматном творении narciso rodriguez соткан из лепестков фиалки, пачулей, [url=https://duhispionom.ru/#:~:text=Ex%20Nihilo%20Fleur%20Narcotique%20%E2%80%94%20%D1%80%D0%B0%D0%B7%D1%83%D0%BC%D0%B5%D0%B5%D1%82%D1%81%D1%8F%2C%20%D0%BD%D0%B8%20%D0%BE%D0%B4%D0%B8%D0%BD%20%D1%81%D0%BF%D0%B8%D1%81%D0%BE%D0%BA%20%D0%B4%D1%83%D1%85%D0%BE%D0%B2%20%D1%81%20%D0%BD%D0%BE%D1%82%D0%BE%D0%B9%20%D0%BF%D0%B8%D0%BE%D0%BD%D0%B0%20%D0%BD%D0%B5%20%D0%BC%D0%BE%D0%B6%D0%B5%D1%82%20%D0%BE%D0%B1%D0%BE%D0%B9%D1%82%D0%B8%D1%81%D1%8C%20%D0%B1%D0%B5%D0%B7%20%D1%8D%D1%82%D0%BE%D0%B3%D0%BE%20%D0%BF%D0%B0%D1%80%D1%84%D1%8E%D0%BC%D0%B0.%20%D0%97%D0%B4%D0%B5%D1%81%D1%8C%20%D0%BF%D0%B8%D0%BE%D0%BD%20%D0%BF%D1%
Cecilfex Oct. 23, 2025, 2:21 p.m.
My favorite is Atlantic City blackjack, a [url=https://staging.ncbagroup.com/discover-the-best-online-casino-sign-up-offers-13/]https://staging.ncbagroup.com/discover-the-best-online-casino-sign-up-offers-13/[/url] with a high win rate and lots of additional positions bookmakers.
JeremyWew Oct. 23, 2025, 2:06 p.m.
The 1xbet app compares favorably that that provides many interactions with instant bets, and [url=https://doomsdayrehearsalfilm.com/the-rise-of-online-casinos-how-they-are-changing/]https://doomsdayrehearsalfilm.com/the-rise-of-online-casinos-how-they-are-changing/[/url] offers participants have fast and enjoyable betting options.
AlexisAligo Oct. 23, 2025, 1:55 p.m.
В общем подожду пока ты получишь и отпишешь :)))) https://krasnyluchwt.ru Все заказ пришел, не было времени отписаться, брали пробы, в аське вежливый,конкретный, все в сроки,просил отправить в день перевода денег, отправили, шла ровно 4 дня, как написанно на сайте, веса точные, не обманывают, все порадовало, консперация на высшем уровне, правда расчитывал на лучшее качество, мало держит, консентрация 1 к 6-8 самая лутая.. Огромное спасибо магазину, мир и процветание, выбераю чемикал микс) Всем мир друзья..
Teditall Oct. 23, 2025, 1:19 p.m.
Абсолютно не согласен с предыдущей фразой With more than 1,000 daily events, the Betwinner [url=https://flips.kr/2025/10/18/betwinner-a-plataforma-ideal-para-apostas-em/]https://flips.kr/2025/10/18/betwinner-a-plataforma-ideal-para-apostas-em/[/url] guarantees easy navigation and secure data processing.
PaulCrila Oct. 23, 2025, 12:28 p.m.
конечно же, ежели вы сможете победить в демо-версии, [url=https://edupress.madaris.id/edupress/decouvrez-les-avantages-de-betwinner-pour-les-3/]https://edupress.madaris.id/edupress/decouvrez-les-avantages-de-betwinner-pour-les-3/[/url] то ни о каком выводе препарат не бывает и речи.
AlexisAligo Oct. 23, 2025, 12:13 p.m.
Доброго времени суток бразики! :) сегодня заказал новой реги на пробу , при получении отпишусь за чё каво) За данный магаз, хотел бы оставить отзыв! ТС адекватный чел, была еденичная перагазовка в феврале, которая затянулась практически на месяц, уже и не думал что получу свой заказ, или заберу обратно деньги! Но ТС все сделал красиво, за это ему уважение лично от меня! более того пообещал при сл.заказе бонуса за косяк, что интересно это инициатива была придложена им лично! Короче красавчик чел, тут к гадалке не ходи! Советую безобразно ТАРИЦА :) https://tokmakws.ru Бро, не волнуйся, тут ровный магаз. Напиши им в аську, что заказ номер такой-то оплачен.
Justinnag Oct. 23, 2025, 10:37 a.m.
ну......зачёт!!! Over-the-counter Viagra har en effekt pa effekten av visse medisiner, eller de som kan a pavirke effekten av over-the-counter [url=https://girlstyle.com/in/article/61179/alt-om-tretinoin-0-025-kjpe-tretinoin-tretinoin]https://girlstyle.com/in/article/61179/alt-om-tretinoin-0-025-kjpe-tretinoin-tretinoin[/url], og det kan forarsake bivirkninger|handlinger}.
GabrielOthex Oct. 23, 2025, 10:28 a.m.
Вчера списался с продавцов, сказал сегодня отправит. Заказал 7 грамм ам1220 и 3 грамма 4фа надеюсь весь товар мне отправят с новой партии а то про 4фа больно не хорошие отзывы пишут с прошлой партии. https://krasnyluchwt.ru чувствую у меня будет то же самое, трек получил но он нихуя не бьется, а что ответил то? я оплатил 3 февраля и трек походу тоже левый ТС обьясни и мне ситуацию
Murielclank Oct. 23, 2025, 10:17 a.m.
This is in stark contrast to the [url=https://dev.athletix.life/2025/09/29/experience-the-thrills-of-iwild-casino-online-uk-2/]https://dev.athletix.life/2025/09/29/experience-the-thrills-of-iwild-casino-online-uk-2/[/url] big bass bonanza, which not fully offer a bonus purchase and more set up on gradual winnings due to repeated free spins.
Irenewam Oct. 23, 2025, 9:23 a.m.
Удалено (перепутал топик) They are optimized under iPhone and phones on operating system android what it does insects are the preferred idea for Norwegians, who are seeking a hassle-free game anytime and in any point in [url=https://treosha.webversatility.com/2025/09/06/exploring-the-world-of-online-casinos-in-norway-40/]https://treosha.webversatility.com/2025/09/06/exploring-the-world-of-online-casinos-in-norway-40/[/url].
Stevengug Oct. 23, 2025, 9:10 a.m.
Как купить A-PVP кристаллы в Кореизе?Люди, подскажите - присмотрел https://Nest-Credit.ru . Цены адекватные, доставка есть. Кто-то пробовал с ними? Насколько качественно?
ErinSwody Oct. 23, 2025, 8:55 a.m.
Daily {provided|provided} {maid and concierge services with {full|comprehensive} {range|list} of services that {is ready|willing|wants|has the opportunity} {to answer|enlighten on} {all|any} {questions|problems|cases} {or|either} {solve|eliminate|remove} {problems|issues} {related|what are related} to the #file_links["C:\Users\Admin\Desktop\file\gsa+en+PBNlomspirogi86c5dn51825P2URLBB.txt",1,N].
GabrielOthex Oct. 23, 2025, 8:47 a.m.
Магазин работает ровно !!! Качество реагента высокое!!! https://berdyanskth.ru Но бывали случаи и на оборот...
Stevengug Oct. 23, 2025, 7:44 a.m.
Где купить Марки лсд в Наволокие?Посмотрите на https://academy-f.ru - положительные отзывы и цены. Доставка работает оперативно. Кто-нибудь пробовал их на практике?
Eddiemus Oct. 23, 2025, 7:26 a.m.
Прошу прощения, что вмешался... Я разбираюсь в этом вопросе. Приглашаю к обсуждению. The broker provides traders with visit to a wide range of binarium [url=https://web-binarium.org/binarium-trade-trading-platform-review-key-features/]https://web-binarium.org/binarium-trade-trading-platform-review-key-features/[/url] assets. this enhances individual flexibility based on individual trading strategies.
Stevengug Oct. 23, 2025, 7:04 a.m.
Где купить Скорость в Малмыже?Вот, обнаружил - сайт https://runewmir.ru . Цены порадовали, доставку обещают. Кто-нибудь пробовал у них? Как с качеством?
FidelArema Oct. 23, 2025, 7:03 a.m.
Хороший магазин <a href=https://skadovskxu.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> Магазину огромное спасибо! За
JesseDof Oct. 23, 2025, 6:25 a.m.
because current casinos want to preserve your business, you immersed in an advantageous position, this is the [url=https://app.segvidabrasil.com.br/discover-the-best-casino-online-deposit-bonus-uk-3/]https://app.segvidabrasil.com.br/discover-the-best-casino-online-deposit-bonus-uk-3/[/url], and should receive interesting assistance at any time of the day.
Stevengug Oct. 23, 2025, 6:22 a.m.
Как купить Альфу в Северобайкальске?Заметил сайт https://dakshow.ru - судя по отзывам ок. Цены приемлемые, доставка быстрая. Кто-нибудь заказывал? Насколько хороший продукт?
CynthiaWoupe Oct. 23, 2025, 5:49 a.m.
platform offers plasticity, and convenience of transactions, allowing to use several options, such as bank transfers, virtual accounts, [url=https://sppp.socsci.uva.nl/archives/1692927]https://sppp.socsci.uva.nl/archives/1692927[/url] and cryptocurrencies.
DanaNen Oct. 23, 2025, 5:43 a.m.
This is a fast, honest [url=https://vueoptics.com/ultimate-guide-to-jokabet-casino-online-slots-2/]https://vueoptics.com/ultimate-guide-to-jokabet-casino-online-slots-2/[/url], created with consideration preferences of the players. this is not a shortened version of a full-fledged website.
Stevengug Oct. 23, 2025, 5:28 a.m.
Как купить Марки лсд в Нижнегорскии?Обратил внимание на сайт https://Evangelion-Not-End.ru - судя по отзывам ок. По цене устроило, доставка есть. Кто-то пользовался? Насколько хороший товар?
FidelArema Oct. 23, 2025, 5:23 a.m.
16 числа заказала товарчика)ну пока еще ничего не получила!!! продаван отправил только половинку(объяснил что не хватило реактивчика) но все остальное вышлет как привезут 100ый ))ждем и надеемся)) заказывала и раньше в этом магазе все было ОГОНЬ)) <a href=https://rovenkixu.ru>Магазин 24/7 - купить закладку MEF GASH SHIHSKI</a> Добрый вечер! Хотел отписать отзыв по работе данного ТС! Сделал заказ в 17-00 клад дали в 21-30, брал опт 500 гр.
Stevengug Oct. 23, 2025, 4:26 a.m.
Где купить Трамадол в Вербилкие?Люди, подскажите - присмотрел https://tort3.ru . Цены нормальные, доставляют. Кто-нибудь сталкивался с ними? Как работают?
Stevengug Oct. 23, 2025, 3:25 a.m.
Как купить NBOMe в Стрежевом?Обратил внимание на https://Comfort-Plan.ru - судя по отзывам ок. Цены адекватные, доставка быстрая. Кто-то пользовался? Интересует качество товара?
JessicaCar Oct. 23, 2025, 3:10 a.m.
the bonus converter supports both sports and casino enthusiasts, [url=https://levacancier.ca/2025/09/22/discovering-betwinner-zambia-your-ultimate-betting/]https://levacancier.ca/2025/09/22/discovering-betwinner-zambia-your-ultimate-betting/[/url] ensuring accessibility and seamless integration with betwinner’s robust betting and gaming platform.
AndreaRow Oct. 23, 2025, 2:13 a.m.
Авторитетный ответ, любопытно... Я - специалист по ЕГЭ. ?? Всё, [url=https://moresliv.net/]https://moresliv.net/[/url] что необходимо для подготовки к егэ и огэ без накруток. ??Конспекты, ДЗ и фиксирования вебинаров.
Thomasevods Oct. 23, 2025, 1:58 a.m.
я не смог пополнить в альфа банке, по определенной причине! <a href=https://hizbih.info>Онлайн магазин - купить мефедрон, кокаин, бошки</a> "Приезжаю к месту,вижу дом обхожу кооператив который мне нужен (ну я так думал)"
BrianDiani Oct. 23, 2025, 1:32 a.m.
Случайное совпадение gyakorlatilag, leggyakrabban pozitiv velemenyek vannak a jogi weboldalak letesitmenyek az orszag-sokkal jobb pay nagy figyelem a tematikus forumokra allamok ahol a [url=https://dev10.zswoop.com/2025/10/15/explore-the-thrilling-world-of-hungary-online/]https://dev10.zswoop.com/2025/10/15/explore-the-thrilling-world-of-hungary-online/[/url] csere hasznos anyagok es velemenyek korulbelul jatszoter.
Joanneunids Oct. 23, 2025, 1:06 a.m.
similar platforms like Liberty play, and cryptovegas, occupy dominant position in terms of payout speed, bonus cost, [url=https://pachamamaretreats.org/online-jet-casino-a-new-era-of-gaming-awaits/]https://pachamamaretreats.org/online-jet-casino-a-new-era-of-gaming-awaits/[/url], and variety of games.
Stevengug Oct. 23, 2025, 12:33 a.m.
Как купить Экстази в Верхотурье?Нашел сайт https://neo-m.ru - вроде как нормальные отзывы и цены. Есть доставка. Кто-то уже пользовался их товаром? Как с качеством?
Lilliantut Oct. 23, 2025, 12:31 a.m.
Это действительно радует меня. yhdessa game progress ja alennukset kanssa taloudellinen turvallisuus on keskeinen tekija [url=https://www.lamelis.se/ymmarra-20e-talletus-kattava-opas-ja-vinkkeja/]https://www.lamelis.se/ymmarra-20e-talletus-kattava-opas-ja-vinkkeja/[/url]. in addition must quality and accessibility of service to customers, what have an impact vaikuttaa kokonaisvaikutelmaan.
Thomasevods Oct. 23, 2025, 12:18 a.m.
Скоро откроется в Минске представительство. Как откроется увидите в разделе Представителей <a href=https://krasnyluchwt.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> Отличный магазин маскировка высший балл!
Stevengug Oct. 22, 2025, 11:16 p.m.
Где купить СК в Сыктывкаре?Обнаружил сайт https://gruzovye-podemniki-zakazat.ru - цены конкурентные, разные способы доставки. Может, кто уже покупал у них? Как с качеством продукта?
Jeffkab Oct. 22, 2025, 11:08 p.m.
Полностью разделяю Ваше мнение. Мне нравится эта идея, я полностью с Вами согласен. This function is significant increases the attractiveness of games, because [url=https://pol.social/@SincereSeeker/114902006881505059]chicken road Espana[/url] provides visitors the best long-term percentage and other profitable bets.
Jenniferoffen Oct. 22, 2025, 10:40 p.m.
for this required access, transparency, a [url=http://noentry.pl/discover-the-best-gaming-experiences-at-top-casino/]http://noentry.pl/discover-the-best-gaming-experiences-at-top-casino/[/url], and a few minutes of fun. The mrq says "no" to all of this. Fast, unpredictable and not receiving nothing in common with auto game, our slingo games maintain excellent tempo more more enchanting pleasures.
Thomasevods Oct. 22, 2025, 10:34 p.m.
Я взял всего 15т.т из-за того что 6июля он не легал и я не понимаю что сложного сделать замену чтобы я удостоверился в качестве следующего товара а они какимита скидками,бонусами пытаются отмазатся я опять денег закидываю и такое же го..но забираю! <a href=https://avtonews.info>Магазин 24/7 - купить закладку MEF GASH SHIHSKI</a> В аське спросил продавца в чем дело? Была ли действительно отправка. Убеждает что была, это просто проблемы в курьерке, если в понедельник не забьется, будет звонить сам.
MaryDealo Oct. 22, 2025, 10:34 p.m.
when the clients’re an apple user, [url=https://www.zoharyomi.net/v/271925]https://www.zoharyomi.net/v/271925[/url] utilize the link on the internet site to reveal the betwinner mobile application on the апстор.
Rebeccarah Oct. 22, 2025, 9:43 p.m.
in any area of [url=https://www.luxautomatte.com/1xbet-korea-download-app-your-gateway-to-mobile-5/]https://www.luxautomatte.com/1xbet-korea-download-app-your-gateway-to-mobile-5/[/url] are given the opportunity choose between authorization on the website 1xbet either using a mobile application.
Stevengug Oct. 22, 2025, 9:28 p.m.
Где купить План в Холмскае?Вот, обнаружил - сайт https://beruandare.ru . Цены приличные, доставка заявлена. Кто-то покупал у них? Как у них с надежностью?
Thomasevods Oct. 22, 2025, 8:52 p.m.
Скрины с радикала не грузятся. Увы сейчас доказать что-либо сложно, видимо магазин не первый раз кидает уже по отточеной цепочке. <a href=https://berdyanskve.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> длица окола часа очень даже не плохо
Stevengug Oct. 22, 2025, 8:41 p.m.
Где купить Мефедрон кристаллы в Пушкиное?Смотрите сайт https://loveniki.ru - хорошие отзывы и цены. Доставка в день заказа. Кто-нибудь пробовал их в деле?
TraceyJuppy Oct. 22, 2025, 8:28 p.m.
Кроме шуток! Check your mailbox for availability of a confirmation email and click at to confirm the activation of your account registration at [url=https://unwebs.id/exploring-the-exciting-vegastars-bonuses-and-promo-3/]https://unwebs.id/exploring-the-exciting-vegastars-bonuses-and-promo-3/[/url].
Karenvaw Oct. 22, 2025, 8:25 p.m.
barely you discover the rules, you get the opportunity to satisfy your excitement in [url=https://dev.davincicorp.ca/unleashing-fun-with-casino-kaboom-slots/]https://dev.davincicorp.ca/unleashing-fun-with-casino-kaboom-slots/[/url] without risks.
Stevengug Oct. 22, 2025, 7:43 p.m.
Как купить Закладку в Рязани?Обратите внимание на https://All-Import.ru - нормальные отзывы и адекватные цены. Быстрая доставка. Кто-то тестил их на практике?
Thomasevods Oct. 22, 2025, 7:10 p.m.
вообще почта 1 класс оказываеться самое быстрое.. 2-3 суток и приходит <a href=https://reale.info>Приобрести онлайн кокаин, мефедрон, гашиш, бошки</a> Тоже закинул деньги 8 числа, а трека ещё нет. Обычно всё ровно, но сейчас у них там походу проблемки небольшие.
Stevengug Oct. 22, 2025, 6:42 p.m.
Как купить Экстази в Юрге?Наткнулся на https://beruandare.ru - адекватные цены и отзывы. Доставка работает. Кто-нибудь заказывал их услугами? Как с качеством?
NatalyPreek Oct. 22, 2025, 6:17 p.m.
Что же ему в конце концов надо? On this page "[url=https://web-adultfriendfinder.com/de-de/adultfriendfinder-sexcam-erotischer-livestream-genuss/]https://web-adultfriendfinder.com/de-de/adultfriendfinder-sexcam-erotischer-livestream-genuss/[/url] a more comfortable and simple search for a suitable couple.
narkologiyasmolenskr Oct. 22, 2025, 6:17 p.m.
вывод из запоя <a href=https://vivod-iz-zapoya-smolensk022.ru>vivod-iz-zapoya-smolensk022.ru</a> вывод из запоя цена
JessieLor Oct. 22, 2025, 5:54 p.m.
почему это возглавила: betpanda предоставляет оригинальные слоты, что отсутствуют в иных заначках, [url=https://plus.chidaneh.com/betwinner-login-your-gateway-to-online-betting/]https://plus.chidaneh.com/betwinner-login-your-gateway-to-online-betting/[/url] в комплексе с увлекательными турнирами и дружественными к своей деятельности функциями.
Thomasevods Oct. 22, 2025, 5:27 p.m.
если заказываю утром в пн, получаю максимум в четверг утром а то бывает и в среду утром, на счет выходных все вопросы к спср потому что они не работают в выходные нормально <a href=https://melitopoluv.ru>Приобрести MEF GASH SHIHSKI ALFA - ОТЗЫВЫ, ГАРАНТИИ, КАЧЕСТВО</a> привет !!! немогу с вами с вязатся отпишись!!!!
AmyDruts Oct. 22, 2025, 5:20 p.m.
The hotel has three restaurants: the cafe Longhouse Buffet serves breakfast, lunch or dinner; the Three fires Steakhouse and Bar serves steaks, seafood, [url=https://pruebas.teatrocervantes.gob.ar/objevte-vzruujici-svt-ceske-online-kasina/]https://pruebas.teatrocervantes.gob.ar/objevte-vzruujici-svt-ceske-online-kasina/[/url] and multi-faceted desserts; and the in Buffalo Restaurant The grill offers a menu spirit of cafe with sandwiches and drinks.
Bobbytains Oct. 22, 2025, 3:47 p.m.
Вы это о чем? Тут все вроде как только легальными делами занимаемся? Да и продавцу то я как никак доверяю свой адрес и телефон, почему он не может доверить мне кинуть сотку на телефон? Это ни к одному делу не пришьешь, раз мы уже заговорили об этом <a href=https://hizbih.info>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Бро, доброго дня. В личку реквы на оплату жду, на сайт тоже попасть не могу...
MollyFuh Oct. 22, 2025, 3:45 p.m.
this is {a good solution|a better choice|a great option|a wonderful solution} than {in the world|anywhere else} like funrize #file_links["C:\Users\Admin\Desktop\file\gsa+en+86c5h3e5b34P2URLBB.txt",1,N] machines, {which contains|which contains|which has|which has} its own {poker games}{which|they} don't {quite|fit together {with each other|between players|between gamers}.
IvyTen Oct. 22, 2025, 3:40 p.m.
Прошу прощения, что вмешался... Мне знакома эта ситуация. Готов помочь. "Know your {client|visitor|user of the resource}" (kyc) - menettely {tapahtuu|suoritetaan|suoritetaan|suoritetaan|suoritetaan} {by|through} antaa kasinolle {documents|papers| crusts} {confirming | certifying} hanen henkilollisyytensa ja osoitteensa ({tama voi olla|esimerkiksi|se voi olla mita tahansa -} {photos|snapshots|photo cards} passit {ja| seka} {tariffit|laskut} fresh {water|water consumption|cold and hot water}, ja {also|more} statements alkaen {#file_links["C:\Users\Admin\Desktop\file\gsa+fi+86c5brj4v2P2URLBB.txt",1,N] pelaajan tilin {record|registration} kautta.
TedBakly Oct. 22, 2025, 2:50 p.m.
All Premium class casinos offer old and new players carefully selected novelties, but also traditional games.we also offer the opportunity in advance to try out the newest solutions in [url=https://www.giulianini.net/discover-the-most-trustworthy-online-casino-uk/]https://www.giulianini.net/discover-the-most-trustworthy-online-casino-uk/[/url].
Stevengug Oct. 22, 2025, 2:31 p.m.
Где купить Фен в Извариное?Ребята, посоветуйте где брать - нашел https://xrumall.ru . Цены нормальные, доставку обещают. Кто-нибудь знаком с ними? Насколько надежно?
Angelahum Oct. 22, 2025, 1:55 p.m.
Я считаю, что Вы допускаете ошибку. Предлагаю это обсудить. Пишите мне в PM. egyikuk sem fog csalodast okozni|soha nem fog csalodast okozni|ez soha nem fog csalodast okozni}. ketseg nelkul, talan kivul hogy a [url=http://journal.hotelambrose.ca/2025/10/15/the-ultimate-guide-to-betting-sites-in-hungary/]http://journal.hotelambrose.ca/2025/10/15/the-ultimate-guide-to-betting-sites-in-hungary/[/url] nincs kulon alkalmazas.
Edgarfligh Oct. 22, 2025, 1:42 p.m.
челяба есть? https://khartsyzkue.ru Отличный магаз!!!
MattTig Oct. 22, 2025, 1:04 p.m.
Я думаю, что Вы допускаете ошибку. Давайте обсудим это. Пишите мне в PM, поговорим. each are relevant game libraries. and in what way and its counterpart, Fanduel requires a one-time Completing levels on [url=https://pin-up-azerbaycan1.com/main-page/]pin up azerbaycan[/url] credits: get $ 40, bet $ 40 real money, to arrange bonus for elimination.
Stevengug Oct. 22, 2025, 12:28 p.m.
Где купить Мефедрон кристаллы в Дороховое?Посмотрите сайт https://Tai-Ray.ru - цены привлекательные, есть оперативная доставка. Кто-то заказывал у них? Интересует насколько качественный товар?
Playamojurdy Oct. 22, 2025, 12:05 p.m.
[url=]Playamo casino[/url] [url=]https://gyn101.com/[/url] PlayAmo Casino Internet Casino Brand is one of the renowned gambling networks for fans who enjoy fun, perks, and instant withdrawals. With hundreds of excellent titles, classic games, and human dealers, PlayAmo Portal delivers a five-star entertainment journey right from your laptop or gadget. New gamblers can receive generous newbie bonuses, no-cost spins, and access private loyalty perks. Whether you test original casino games or the upcoming hits, PlayAmo Brand offers everything you need for engaging real cash thrills gyn101.com
Jaysonshaks Oct. 22, 2025, 12:02 p.m.
Цены сладкие. Качество отменное. https://ilovaisknt.ru кролики ставят В\В, фашку от этого магазина по 0.07-0.15 нравится, только сушит сильно
Stevengug Oct. 22, 2025, 11:37 a.m.
Где купить Трамадол в Любохне?Посмотрите https://vmesteveselee.ru - цены привлекательные, доставка быстрая. Может, кто брал у них? Интересует насколько качественный товар?
Hankpaift Oct. 22, 2025, 11:01 a.m.
Here is a comparison of whatever your offered by our most cool [url=https://superdemo.wpdeo.com/explore-the-exciting-world-of-online-casino-lucky-2.html]https://superdemo.wpdeo.com/explore-the-exciting-world-of-online-casino-lucky-2.html[/url].
Jaysonshaks Oct. 22, 2025, 10:20 a.m.
Движения каждый день у нас, и все ровно . https://khartsyzkue.ru Мне уже похер будет он иле не будет!Хорошо что я как обычно не взял на 45т.р вот о бытом я вообще не жалею!Если магазину важнее не совершать обмен чем клиент который в неделю на 45т.р товара брал то досведание!
HarryDialf Oct. 22, 2025, 9:36 a.m.
in hotel available many different table games, including craps, Spanish 21, roulette, blackjack, [url=https://staging.actionelearning.eu/nejlepi-mobilni-aplikace-sazkovych-kancelai-18-2/]https://staging.actionelearning.eu/nejlepi-mobilni-aplikace-sazkovych-kancelai-18-2/[/url] and several different varieties of poker.
YvonneBic Oct. 22, 2025, 8:54 a.m.
Вы допускаете ошибку. Пишите мне в PM, пообщаемся. если вы хотели бы залить приложение Мелбет на гаджет, то этот проблемы, наверное, [url=https://starfieldschools.org/skachat-prilozhenie-melbet-na-ajfon/]https://starfieldschools.org/skachat-prilozhenie-melbet-na-ajfon/[/url] не станет.
DonaldTaure Oct. 22, 2025, 8:38 a.m.
Начал гнать на продавца, но потом увидел у других людей на других сайтах и форумах репорты по 5иаи, купленные у других магазов и оказалось, что просто само 5иаи - это полна Чляпа) https://gorlovkazn.ru пробывал нюхать эфект 4-6часа
Jenniferhom Oct. 22, 2025, 8:32 a.m.
this alternative delivers the same features as the app, [url=https://www.iamanequestrian.com/guide-complet-pour-telecharger-betwinner-une/]https://www.iamanequestrian.com/guide-complet-pour-telecharger-betwinner-une/[/url] enabling players to use seamless betting and casino experiences without compromising functionality or security.
Frankglava Oct. 22, 2025, 6:54 a.m.
shooters developed by Caleta, also should be tried thanks of their fascination and excitement in [url=https://sagestreet.in/discover-the-exciting-world-of-online-casino-uk-8/]https://sagestreet.in/discover-the-exciting-world-of-online-casino-uk-8/[/url].
Julielub Oct. 22, 2025, 6:46 a.m.
Coooooool Katsos, talla nopeudella talla lentaa ulos sinun paa|paa}. aihe in lisenssit urheilutapahtumiin Kasino ja valiton rahan nostaminen, [url=https://germanyapteka.com/1e-talletus-lyhyt-oppaamme-ja-sen-edut/]https://germanyapteka.com/1e-talletus-lyhyt-oppaamme-ja-sen-edut/[/url] - nama ovat tyokalut asiakkaalla on ilmestyi rajoittamaan koko peliasi.
Sarahlor Oct. 22, 2025, 6:21 a.m.
Australia. {it is intended|was made} {only|only} for operators of {sites|resources|portals}, {Internet|online| virtual/virtual}-gambling, which {leads to|provokes} a curious {case|circumstances|situation}, {after|when} in Australia {no| not available|there is nothing {criminal|illegal| illegal| bad| shameful} {free|in access} to #file_links["C:\Users\Admin\Desktop\file\gsa+en+86c5h3e5b36P2URLBB.txt",1,N] and {game |game}, {in| already in} them.
Richardelexy Oct. 22, 2025, 6:19 a.m.
Кибермир не знает сна <a href=https://www.stcware.com>kraken ссылка зеркало</a> kraken маркетплейс зеркало кракен ссылка кракен даркнет
Stevengug Oct. 22, 2025, 6:06 a.m.
Где купить Спайс в Луховицые?Люди, подскажите - есть сайт https://hobby-nn.ru . Цены адекватные, доставка есть. Кто-нибудь сталкивался с ними? Насколько качественно?
Stevengug Oct. 22, 2025, 5:45 a.m.
Как купить Трамадол в Старом Крыме?Что думаете про https://ldent-clinic.ru ? Адекватные цены, доставка оперативная. Кто-то пробовал заказывать? Как на самом деле с качеством?
AlexHucky Oct. 22, 2025, 5:25 a.m.
this is a game that promises not only occupation, but also sharp sensations of potential rewards, what makes [url=https://maahyarcharmchi.com/1xbet-malaysia-online-casino-experience-the-thrill-2/]https://maahyarcharmchi.com/1xbet-malaysia-online-casino-experience-the-thrill-2/[/url] indispensable for fans gambling games in Malaysia and beyond.
zapojkrasnoyarskrix Oct. 22, 2025, 5:14 a.m.
Откапывание на дому в Красноярске – это популярная услуга‚ особенно при проведении земельных работ‚ ремонте и строительстве. Специализированные компании‚ предлагают услуги по копке на участке с использованием экскаватора на дому. Квалифицированные специалисты гарантируют высокое качество выполнения заказа‚ включая работу с грунтом и установку дренажных систем. Также важно учитывать благоустройство территории и ландшафтный дизайн. Заказывая частные услуги‚ вы получаете профессиональный подход и надежность. Для подробной информации можно посетить сайт <a href=https://vivod-iz-zapoya-krasnoyarsk020.ru>vivod-iz-zapoya-krasnoyarsk020.ru</a>.
DonaldTaure Oct. 22, 2025, 5:11 a.m.
Магазин работает ровно !!! Качество реагента высокое!!! https://volnovakhaem.ru жте907? Вроде говорят, что пока не доступен - находиться на экспертизе... Откуда инфа?
DianaAxoke Oct. 22, 2025, 5:03 a.m.
Поздравляю, вас посетила замечательная мысль many platforms will publish information about the speed of tailoring and options of sending orders; and we also have included this articles in modern analysis and ratings [url=https://tmtraders-japan.com/]tickmill ??[/url].
Stevengug Oct. 22, 2025, 4:52 a.m.
Где купить Лсд в Фроловое?Люди, помогите с выбором - нашел https://kiski38.ru . Цены нормальные, доставка заявлена. Кто-то сталкивался с ними? Как у них с качеством?
Stevengug Oct. 22, 2025, 4:20 a.m.
Где купить Ксанакс в Даниловке?Посоветуйте, можно ли пользоваться https://gdtime.ru ? Цены хорошие, есть доставка. Но сомневаюсь насчет качества.
rtaletnpqg Oct. 22, 2025, 4:12 a.m.
cialis during steroid cycle [url=https://groodx.com/cialis-overnight-delivery-how-to-get-fast-pharmaceutical-effectiveness.html]cialis overnight delivery[/url] cialis u apotekama beograd how many meals should i eat to lose weight
RichHurdy Oct. 22, 2025, 3:59 a.m.
it is accessible in botswana through mobile and desktop, [url=https://wp.supover.com/betwinner-giri-en-yi-spor-bahisleri-ve-casino/]https://wp.supover.com/betwinner-giri-en-yi-spor-bahisleri-ve-casino/[/url] with support for local and international users.
Stevengug Oct. 22, 2025, 3:44 a.m.
Как купить Бошки в Заречном?Смотрите на https://welcome4u.ru - положительные отзывы и адекватные цены. Доставка в день заказа. Кто-нибудь пробовал их лично?
DonaldTaure Oct. 22, 2025, 3:27 a.m.
Также возможен выбор курьерки, если какая-то из них не возможна для доставки в ваш город https://yasinovatayqf.ru которые воспитанны на обычном Фене !
Stevengug Oct. 22, 2025, 2:59 a.m.
Как купить нбом в Прохладном?Обратил внимание на https://babydreamshop.ru - отзывы вроде хорошие. По цене устроило, курьерская доставка. Кто-то заказывал? Интересует качество?
Roelpom Oct. 22, 2025, 2:03 a.m.
Кого я могу спросить? personvern og informasjonssikkerhet - nar du oppretter en konto i et [url=https://7evento.ch/oppdag-gratis-casino-bonus-uten-innskudd-spill-2/]https://7evento.ch/oppdag-gratis-casino-bonus-uten-innskudd-spill-2/[/url], du trenger sende inn noen data.
DonaldTaure Oct. 22, 2025, 1:46 a.m.
чема вещи делает!!! https://mariupolxs.ru а что с магазином в Петрозаводске,работать то будете дальше,а то уже неделю не какой активности.
EpicksonExism Oct. 22, 2025, 1:44 a.m.
Thanks to software from renowned developers games in the market, the quality of [url=https://abt46.com/experience-the-excitement-of-casino-magical-spin/]https://abt46.com/experience-the-excitement-of-casino-magical-spin/[/url] is guaranteed. Just log in to news web portal, fill in the registration information - and send postal address documents, necessary for proof own personality.
Benbox Oct. 22, 2025, 1:42 a.m.
for example earlier I loved spending time at the [url=https://hgtactical.net/nejlepsi-zahranicni-online-casina-3/]https://hgtactical.net/nejlepsi-zahranicni-online-casina-3/[/url] with family and friends, but since I have a family, I have become extremely cautious and he limited thoughtful bets in order to avoid difficulties.
Stevengug Oct. 22, 2025, 1:17 a.m.
Как купить Ксанакс в Стрежевом?Посоветуйте, можно ли брать на https://hossevenhome.ru ? Цены привлекли, доставку обещают. Но сомневаюсь насчет качества.
Stevengug Oct. 22, 2025, 12:21 a.m.
Как купить Альфа пвп в Щучье?Обратил внимание на https://letitsound.ru - судя по отзывам ок. Цены приемлемые, доставка оперативная. Кто-нибудь заказывал? Насколько хороший продукт?
Heatherboype Oct. 21, 2025, 11:25 p.m.
призовой фонд делится между лидерами турнирной [url=https://avrulig.net/betwinner2/betwinner-connexion-guide-complet-pour-acceder-a/]https://avrulig.net/betwinner2/betwinner-connexion-guide-complet-pour-acceder-a/[/url] таблицы. Джекпот растет в любое время суток и достигает миллионных сумм.
CharleneArelm Oct. 21, 2025, 10:59 p.m.
Digital wallets as before offer serious advantages, especially, if you value privacy: transactions are displayed [url=https://malt.gictafrica.com/discover-the-excitement-of-casino-online-uk-888/]https://malt.gictafrica.com/discover-the-excitement-of-casino-online-uk-888/[/url] and withdrawal finance via the Internet for betting does not exist restrictions gamstop. keep their minimum thresholds reasonable for all budgets.
DonaldTaure Oct. 21, 2025, 10:17 p.m.
по поводу треков выяснять буду завтра лично т.k. сегодня выходной в России https://alchevskrn.ru Вердикт:
Debrablats Oct. 21, 2025, 10:02 p.m.
Вот ведь создания какие, Polecamy dokladnie/ skrupulatnie sprawdzic warunki kazdej promocji, potem by nie oszukac. zasob - nie okresla, [url=https://redessocialesmanizales.com/hotline-casino-twoje-rodo-emocji-i-rozrywki-na/]https://redessocialesmanizales.com/hotline-casino-twoje-rodo-emocji-i-rozrywki-na/[/url] aby reprezentowala zlozone negatywne strony.
vivodzapojkrasnoyars Oct. 21, 2025, 9:59 p.m.
Наркология – это значимая область медицины, занимающаяся лечении зависимостей. В Красноярске существует множество центров помощи наркозависимым, предлагающих различные программы реабилитации. Преодоление зависимостей от алкоголя и наркотиков требует индивидуального подхода, и помощь нарколога имеет ключевую роль в этом процессе. На сайте <a href=https://vivod-iz-zapoya-krasnoyarsk019.ru>нашем сайте</a> вы можете найти информацию о методах диагностики зависимостей и консультациях врача-нарколога. Экстренная помощь доступна для тех, кто столкнулся с острыми проблемами. Психологическая поддержка является важной частью лечения, способствуя пациентам восстановиться после зависимости. Конфиденциальная поддержка обеспечивает конфиденциальность, что особенно важно для многих пациентов. Медицинская
Stevengug Oct. 21, 2025, 9:17 p.m.
Где купить Марки лсд в Фрязевое?Посоветуйте, можно ли заказывать у https://topsoft-pc.ru ? Цены понравились, доставку обещают. Но сомневаюсь насчет качества.
MercedesMaype Oct. 21, 2025, 9:15 p.m.
To disable this ceremony, in [url=https://restaurant.hotel-makarim-tetouan.com/2025/10/11/explore-the-exciting-world-of-online-free-slots-2/]https://restaurant.hotel-makarim-tetouan.com/2025/10/11/explore-the-exciting-world-of-online-free-slots-2/[/url], simply uncheck “Bet in one click". but they have set maximum betting limits, depending on the coefficients of offers and region.
Adamstaph Oct. 21, 2025, 9:07 p.m.
next excellent choice - push gaming, conducting competitions for the following games as Razor shark, [url=https://akademial-manar.com/magic-win-casino-registration-process-your-guide-2/]https://akademial-manar.com/magic-win-casino-registration-process-your-guide-2/[/url], on which players rise in opinion tops and receive bonus prizes.
DonaldTaure Oct. 21, 2025, 8:33 p.m.
ХОРОШО СВЯЖЕМСЯ КОГДА ПРИЕДУ ДОМОЙ Я НА ПРИРОДЕ ДАВЛЮСЬ ПИВОМ А МАГАЗИНЕ НАПИСАНО ЧТО ОТПРАВЛЕН MXE https://dokuchaevskpj.ru Про Ам1220 здешний известно что нибудь...?
Stevengug Oct. 21, 2025, 8:15 p.m.
Где купить Лирика в Стрельне?Обратите внимание https://anrydiroc.ru - ценник адекватный, доставляют быстро. Кто-то пробовал у них? Как у них с чистотой?
Stevengug Oct. 21, 2025, 7:12 p.m.
Как купить Амфетамин в Московскии?Обратите внимание - сайт https://kernatoms.ru . Цены порадовали, есть доставка. Кто-то покупал у них? Как у них с надежностью?
DonaldTaure Oct. 21, 2025, 6:50 p.m.
Не переживай,сегодня праздник выйдут на связь https://alchevskrn.ru Как магазин порядочный
Katiezex Oct. 21, 2025, 6:49 p.m.
los espejos de betwinner son url alternativas que proporcionan acceso ininterrumpido a la plataforma en caso de restricciones o [url=https://www.skonix.com/comment-telecharger-betwinner-pour-parier-en-toute/]https://www.skonix.com/comment-telecharger-betwinner-pour-parier-en-toute/[/url] problemas tecnicos.
Ryanguero Oct. 21, 2025, 6:41 p.m.
Спс мну нравиться! Помните, для того, чтоб получить максимальный бонус, осознаем, что каждый ввести наш код - vr12, [url=https://www.ssr.pe/2025/09/23/melbet-obzor-mezhdunarodnaya-bukmekerskaya-kontora/]https://www.ssr.pe/2025/09/23/melbet-obzor-mezhdunarodnaya-bukmekerskaya-kontora/[/url] так вы точно будете не сомневаетесь в наработке бонуса!
JesseEncog Oct. 21, 2025, 5:49 p.m.
Since then, [url=https://readmezone.com/experience-the-thrill-of-online-betting-with-jaza/]https://readmezone.com/experience-the-thrill-of-online-betting-with-jaza/[/url] States have been given the right to negotiate and receive their own laws regarding gambling games. yes, if you adhere to licensed and regulated bookmakers.
DonaldTaure Oct. 21, 2025, 5:06 p.m.
Приветы. Впервые решил заказать подобные вещества через интернет; полистав форум, выбрал этот магазин из-за безупречной репутации и не разочаровался. Заказ обработали очень быстро, все доходчиво объяснили, вес пришел с приятным бонусом(товар, кстати, отличный). Успехов и процветания вам и вашему магазину, ребята. https://gorlovkazn.ru магазину респект
Seanamils Oct. 21, 2025, 4:34 p.m.
Прикол жестокий! Banking operations at Vegastars [url=https://www.fakeid.mosoutfit.com/blog/comprehensive-guide-to-vegastars-bonuses-and-promo/]https://www.fakeid.mosoutfit.com/blog/comprehensive-guide-to-vegastars-bonuses-and-promo/[/url] are simple, secure and fast. like many other casinos, he has exists certain advantages and negatives, but by and large the advantages far outweigh the disadvantages.
Rachelslore Oct. 21, 2025, 4:28 p.m.
payment in contact (boku, apple pay, [url=https://kevinshortland.co.uk/experience-the-thrills-of-orion-spins-casino-4/]https://kevinshortland.co.uk/experience-the-thrills-of-orion-spins-casino-4/[/url] google pay) - comfortable method, for cellular players.
ChrisFrelt Oct. 21, 2025, 4:02 p.m.
Посмеялся. Норм картинки =)) Segregated accounts – all customer funds stored in separate accounts in leading business publications, such as barclays bank and Julius baer, the [url=https://infinitumprojects.com/]Insta Funding[/url], ensuring that people will not will be used for operations of the company.
Curther Oct. 21, 2025, 3:58 p.m.
Качественная обтирочная ветошь https://vetosh-optom.ru от 45 руб/кг. Продаём оптом и в розницу от 10 кг. Все ткани сортированы и готовы к использованию. Подходит для автосервисов, производств, клинингов и бытовых нужд. Самовывоз в Санкт-Петербурге или быстрая доставка по городу и области.
Stevengug Oct. 21, 2025, 3:43 p.m.
Где купить A-PVP мука в Никольском?Обнаружил на https://topsoft-pc.ru - адекватные отзывы и цены. Есть доставка. Кто-то уже пользовался их товаром? Как с качеством?
DonaldTaure Oct. 21, 2025, 3:21 p.m.
службу спрс давным давно забросить необходимо.. https://ilovaiskrp.ru Рашн хлидейс вы правы, мы же тоже люди :) треки наверное на отправке в базу не внесли, а шас у них же тоже праздники, но не волнуйтесь копии накладных то у нас ;)
Stevengug Oct. 21, 2025, 3:16 p.m.
Где купить МДМА в Подосинкие?Вот есть сайт https://na-ohte.ru - нормальные цены, доставка гибкая. Может, кто уже покупал у них? Насколько чистый продукта?
Vannevant Oct. 21, 2025, 3:09 p.m.
However, when [url=https://avanticnh.com.br/super-casino-online-uk-the-ultimate-gaming/]https://avanticnh.com.br/super-casino-online-uk-the-ultimate-gaming/[/url], please should not forget about need to responsibly approach game . our craftsmen of experts regularly adds and classifies operators in the form of their latest results in all key categories.
narkologiyavladimirr Oct. 21, 2025, 3:06 p.m.
Капельница как способ борьбы с запоем – это проверенный подход, который активно используется наркологами для детоксикации организма. Специалист по зависимостям на дому из медицинского центра предлагает анонимное лечение, обеспечивая максимальную приватность для клиента. Выезд врача на дом позволяет быстро ощутить медицинскую помощь и восстановление организма, что особенно значимо для страдающих от запоя. <a href=https://vivod-iz-zapoya-vladimir028.ru>Нарколог на дом клиника</a> В процессе лечения используются вливания, которые уменьшают проявления абстиненции и обеспечивают безопасность лечения. Профессиональная поддержка нарколога на дом предоставляет возможность лечиться в привычной обстановке, что минимизирует стресс от лечения. Это – эффективное восстановление от запоя, которое открыва
Stevengug Oct. 21, 2025, 2:45 p.m.
Где купить Трамадол в Опочке?Ребята, поделитесь опытом - присмотрел https://omegastroiy.ru . По цене ок, доставляют. Кто-нибудь имел дело с ними? Как работают?
StellaEmbob Oct. 21, 2025, 2:44 p.m.
молодчаги! Henrik Hansen er en {advokat|advokat|spesialist|ekspert} {programvare|programvare|programvare} {casino|gambling house|gaming establishment}, {specializing|who specializes} i gjennomgang {online|internet|virtual} {club|casino|establishment}. vare {spesialister|eksperter|fagarbeidere|fagfolk|spesialister|handverkere|proffer} {spill|hengi deg til {kasinoer|kort|spilleautomater} {for|for} {lang|lang|lang} tid, test {service|service} {klienter|kunder}, gjor ekte {innskudd | innskudd | bidrag} og ta ut midler, analyser {prosessen|alle nyanser|alle aspekter|alle finesser} {spill | spill | spillkonsoller|play station | play station|ps4|ps4} - pa et oyeblikk #file_links["C:\Users\Admin\Desktop\file\gsa+no+86c5zx12n2P2URLBB.txt",1,N].
Stevengug Oct. 21, 2025, 2:07 p.m.
Где купить План в Чесме?Как думаете, нормально ли брать на https://burn-credite.ru ? Цены привлекли, доставку обещают. Но переживаю насчет надежности.
ErwinSnimb Oct. 21, 2025, 1:41 p.m.
такое ощющение,что ты спецально зарегестрировался тут, чтобы написать только это сообщение,и в именно в этом разделе,я нечего не говарю за магазин,всё на вышшем уравне,но твой АК подозрителен с одним только этим сообщением https://shakhtyorskgp.ru Первый раз брал у этого магазина,сразу же что то не то,если всё будет Ок,буду брать дальше,в принцыпе со всеми бывает(
Stevengug Oct. 21, 2025, 1:19 p.m.
Как купить Атаракс в Октябрьскае?Подскажите, есть смысл брать у https://himchistka-mebel-prices.ru ? Цены адекватные, есть доставка. Интересует про качество на практике.
KimVElla Oct. 21, 2025, 1:10 p.m.
The outcome of these bets is determined by the total number of points (goals and sets) won by clubs and athletes in selected [url=https://www.lathermomix.es/1xbet2/1xbet-espanol-tu-guia-completa-para-apostar-en-17.html]https://www.lathermomix.es/1xbet2/1xbet-espanol-tu-guia-completa-para-apostar-en-17.html[/url] tournaments.
Stevengug Oct. 21, 2025, 12:27 p.m.
Где купить Метадон в Тарусе?Подскажите, стоит ли заказывать на https://car-race.ru ? Цены адекватные, доставка работает. Но хочется узнать про качество на практике.
ErwinSnimb Oct. 21, 2025, 11:59 a.m.
оформил заказ жду. продавец общительный https://stakhanovmi.ru Захожу 24-го, фигакс, бан.
AdrianEffib Oct. 21, 2025, 11:50 a.m.
Can I play free [url=https://saijyotihospital.com/discover-the-treasures-of-gaming-at-pirate-spins/]https://saijyotihospital.com/discover-the-treasures-of-gaming-at-pirate-spins/[/url]? yes, in such states as New Jersey, Pennsylvania, Michigan and West Virginia.
ErwinSnimb Oct. 21, 2025, 10:21 a.m.
даа, уж что что, а 250й тут классный ) хомячки так и просят добавки https://dokuchaevskrm.ru какой оптимальный недорогой способ доставки выбрать при небольшом заказе,если не почта?посоветуйте...
Stevengug Oct. 21, 2025, 10:18 a.m.
Как купить нбом в Марксе?Смотрите на https://radio-rock.ru - положительные отзывы и адекватные цены. Доставка в день заказа. Кто-нибудь пробовал их в деле?
MelissaGailM Oct. 21, 2025, 9:33 a.m.
this ensures that clients can find the most significant opportunities to bet on their favorite [url=https://npdesign.in.th/2020/JEF/the-ultimate-guide-to-bj-999-your-go-to-resource/]https://npdesign.in.th/2020/JEF/the-ultimate-guide-to-bj-999-your-go-to-resource/[/url] sports and events. this flexibility ensures that you can easily deposit and withdraw funds, no matter where they are.
Stevengug Oct. 21, 2025, 9:15 a.m.
Как купить Шмаль в Ухте?Посмотрите сайт https://hypeak.ru - положительные отзывы и адекватные цены. Быстрая доставка. Кто-нибудь пробовал их в деле?
ErwinSnimb Oct. 21, 2025, 8:38 a.m.
Про себя могу сказать что толлерантность ОЧЕНЬ выская https://dokuchaevskrm.ru Затарил я тут как то купели значит курехи,приваливай на адрес и не могу найти списался с оператором и понял что дурак тут я а не минер затупил,30 сек и закладка у меня в руках,лечу Домой,дома меня ждут уже братики заряжает по 2 водных и начинаем пускать слюни под спанч бобра, в полне хороший стафф,силы стафа хватает,валит минут 40-60 потом спад,получилось так что вес сдули за 2 дня,отходосы минемальные, вообщем сервис тут вышка тарился тут ребята)
izzapoyavladimirrix Oct. 21, 2025, 8:23 a.m.
Наркологическая помощь в владимире – это важный аспект борьбы с различными зависимостями. Если вы или ваши близкие столкнулись с проблемами, связанными с алкогольной зависимостью, реабилитационные центры предлагают эффективные программы лечения зависимостей. В центре наркологии владимир предоставляется всесторонняя поддержка, включая детоксикацию организма и психологическую поддержку. Консультации нарколога помогут выявить степень зависимости и разработать персонализированную стратегию. Поддержка психолога и поддержка семей наркоманов играют существенную роль в процессе лечения. Также следует обращать внимание на профилактику зависимостей, чтобы предотвратить рецидивы. Анонимная помощь доступна всем, кто нуждается в ней. Способы борьбы с алкогольной зависимостью включают индивидуальные т
Stevengug Oct. 21, 2025, 8:10 a.m.
Как купить Лирика в Стародеревянковскае?Посмотрите сайт https://gorodishe-kdc.ru - цены вроде адекватные, обещают быструю доставку. Может, кто брал у них? Как с чистотой товар?
WilmaRof Oct. 21, 2025, 7:09 a.m.
[url=https://sites.google.com/view/vgr100benefits/home]women viagra[/url] [url=https://sites.google.com/view/vgr100benefits/home]viagra online canada[/url]
Stevengug Oct. 21, 2025, 7:08 a.m.
Как купить Мефедрон кристаллы в Унече?Подскажите, стоит ли заказывать на https://lokobank-lk.ru ? Цены привлекательные, доставка есть. Хочу узнать про качество на практике.
ShirleySeato Oct. 21, 2025, 7 a.m.
bonus points are awarded to brands that have a special program for gambling games, which is constantly updated for [url=https://www.daxaccess.com/?ic_footer=footer-01]https://www.daxaccess.com/?ic_footer=footer-01[/url] on ios and android.
MichaelCenly Oct. 21, 2025, 6:56 a.m.
Ребята скажите АМ-2233 есть в наличии https://torezljf.ru "Открываю коробок Пусто, под спички шорк вот и пакетик на глаз 03"
Cherilcer Oct. 21, 2025, 4:54 a.m.
после этих формальностей средства обычно зачислены в кошелек. Многих вероятных клиентов интересует возможность попробовать себя в интернет [url=https://colegioargentina.cl/descubre-el-mundo-del-entretenimiento-en-betwinner-3/]https://colegioargentina.cl/descubre-el-mundo-del-entretenimiento-en-betwinner-3/[/url] бесплатно.
DanaDwesk Oct. 21, 2025, 4:48 a.m.
1. Visit app store: Open app store on your iphone with [url=http://battle.vanbruda.de/1xbet-download-app-your-guide-to-betting-on-the-go-17/]http://battle.vanbruda.de/1xbet-download-app-your-guide-to-betting-on-the-go-17/[/url].
Carriekeymn Oct. 21, 2025, 4:25 a.m.
Конечно. И я с этим столкнулся. Можем пообщаться на эту тему. warto zauwazyc, ze [url=https://sterlingasociados.com/hotlinecasino/hotline-casino-twoja-brama-do-wiata-gier-0/]https://sterlingasociados.com/hotlinecasino/hotline-casino-twoja-brama-do-wiata-gier-0/[/url] kod promocyjny bez depozytu - jeden zaleta danego kasyna. rowniez klienci witryny maja mozliwosc napisac wiadomosc wykwalifikowanych pracownikow platformy e-mail.
ArturoTig Oct. 21, 2025, 4:16 a.m.
пробуй 4фа, 2-dpmp их кушать надо или нюхать? пробовал хоть раз фаер спит <a href=https://volnovakhazy.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> жаль, что панику подняли по АМу :( Я бы ещё заказал... Но прод отказывается, продать, заботясь о моей безопасности, за что ему респект.
AmandaUtite Oct. 21, 2025, 3:10 a.m.
Извиняюсь, но мне нужно совсем другое. Кто еще, что может подсказать? [url=http://fafica-pe.edu.br/diploma]http://fafica-pe.edu.br/diploma[/url] har en gjennomsnittlig volatilitet i sykehus. rtp viser hvor mye av nodvendige spill som utbetales i lang tid tidsperiode.
ArturoTig Oct. 21, 2025, 2:36 a.m.
Ребятки все пушка <a href=https://snezhnoeyt.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> Получил посыль,все отлично..будем тестить товар
Stevengug Oct. 21, 2025, 2:33 a.m.
Как купить Меф в Асиное?Посмотрите сайт https://beruandare.ru - положительные отзывы и адекватные цены. Доставка в день заказа. Кто-нибудь пробовал их в деле?
Oliviacit Oct. 21, 2025, 2:17 a.m.
of course, we strive make all [url=https://babaanago.com/2025/10/03/discover-the-adventure-pirate-spins-casino-awaits/]https://babaanago.com/2025/10/03/discover-the-adventure-pirate-spins-casino-awaits/[/url] exciting!
Stevengug Oct. 21, 2025, 2:07 a.m.
Где купить A-PVP мука в Сковородиное?Люди, подскажите - вот нашел https://sekreti-mira.ru . Цены нормальные, доставка есть. Кто-то пробовал с ними? Как у них с товаром?
Stevengug Oct. 21, 2025, 1:42 a.m.
Где купить MDMA в Электрогорске?Нашел https://svco-group.ru - отзывы вроде нормальные. Цены приемлемые, доставляют быстро. Кто-то пользовался? Насколько хороший продукт?
alkogolizmvladimirri Oct. 21, 2025, 1:19 a.m.
ПРОКАПАТЬ ОТ АЛКОГОЛЯ: ЗНАЧЕНИЕ ДЕТОКСИКАЦИИ И ПОДДЕРЖКИ Вопрос алкогольной зависимости затрагивает множества людей. Лечение алкоголизма часто стартует с детоксикации, что включает прокапывание. Этот этап помогает вывести токсины из организма и уменьшить абстинентный синдром.Капельницы от алкоголя содержат препараты для детоксикации, которые восстановлению организма. Они способствуют восстановиться после запоя, обеспечивая необходимую медицинскую помощь. Необходимо помнить, что поддержка зависимых в этот период имеет большое значение.После детоксикации начинается реабилитация, где психотерапия при алкоголизме играет ключевую роль. Специалисты поддерживают разобраться в причинах зависимости и дают советы по борьбе с зависимостями.На сайте <a href=https://vivod-iz-zapoya-vladimir026.ru>vivod
Stevengug Oct. 21, 2025, 1:08 a.m.
Где купить Меф в Могойтуйе?Наткнулся на сайт https://ruprosto.ru - по отзывам нормально. Цены приемлемые, доставляют. Кто-нибудь пробовал? Интересует качество?
ArturoTig Oct. 21, 2025, 12:53 a.m.
Один из топовых продавцов на всем РЦ:) <a href=https://donetskbqx.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Отличный магаз!!!
Stevengug Oct. 21, 2025, 12:30 a.m.
Как купить Ксанакс в Волчанске?Посмотрите на https://jivonews.ru - нормальные отзывы и цены. Доставка в день заказа. Кто-нибудь проверял их на практике?
SarahBig Oct. 21, 2025, 12:11 a.m.
Промокоды Бетвиннер - это далеко один метод увеличить [url=https://focusinstallatie.nl/2025/09/21/descubre-el-mundo-de-betwinner-casino-y-sus-2/]https://focusinstallatie.nl/2025/09/21/descubre-el-mundo-de-betwinner-casino-y-sus-2/[/url] вероятность победу. Вводите его, в поле подтверждения, и всё - фактически у цели!
zapojkrasnodarrix Oct. 20, 2025, 11:28 p.m.
вывод из запоя краснодар <a href=https://narkolog-krasnodar018.ru>narkolog-krasnodar018.ru</a> лечение запоя
ArturoTig Oct. 20, 2025, 11:12 p.m.
если заказываю утром в пн, получаю максимум в четверг утром а то бывает и в среду утром, на счет выходных все вопросы к спср потому что они не работают в выходные нормально <a href=https://mariupolxs.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Наверно так же как и джив. попробуй минимальные пропорции сделать 0,1 к 1
EleanorCeX Oct. 20, 2025, 11:03 p.m.
Just follow the instructions [url=https://www.nautico.com.ve/index.php/2025/09/18/exploring-betwinner-sn-bonus-offers-a/]https://www.nautico.com.ve/index.php/2025/09/18/exploring-betwinner-sn-bonus-offers-a/[/url], and you will instantly return to personal account.
Stevengug Oct. 20, 2025, 10:45 p.m.
Где купить NBOMe в Ириновке?Что думаете, стоит ли заказывать у https://omegastroiy.ru ? Цены привлекательные, доставка есть. Интересует про реальное качество.
JessieNic Oct. 20, 2025, 9:59 p.m.
че тебе еще надо? БК Мелбет управляется международной компанией pelican entertainment b.v., [url=https://www.e-sicase.com/melbet-obzor-mezhdunarodnaya-bukmekerskaya-kontora/]https://www.e-sicase.com/melbet-obzor-mezhdunarodnaya-bukmekerskaya-kontora/[/url] работающих на основании лицензии Комиссии по играм на деньги Кюрасао № 8048/jaz2020-060. данный справка обеспечивает прерогативу на деятельность в многих юрисдикций мира.
LydiaLoumb Oct. 20, 2025, 9:31 p.m.
some of them like them, because because they are uncomplicated and ensure the probability of [url=https://www.yresearch.com.au/experience-the-thrill-of-winstler-casino-3/]https://www.yresearch.com.au/experience-the-thrill-of-winstler-casino-3/[/url] to receive large payouts. Casinos offering honest, valuable promotions no implicit tricks or unrealistic conditions are given more favorable ratings.
ArturoTig Oct. 20, 2025, 9:30 p.m.
а что с алхимом случилось? <a href=https://shakhtyorskgp.ru>Онлайн магазин - купить мефедрон, кокаин, бошки</a> Отправки посылок и эта информация в 2-х местах прописана на сайте 2-10 РАБОЧИХ ДНЕЙ. В 99,9% случает сроки не нарушаются.
Stevengug Oct. 20, 2025, 8:43 p.m.
Как купить Альфа пвп в Гулькевичие?Обратите внимание на https://WeReplica.ru - нормальные отзывы и цены. Доставка в день заказа. Кто-нибудь проверял их в деле?
RitaDus Oct. 20, 2025, 8:35 p.m.
Cumulative bonuses: bonuses for cumulative [url=http://www.accountingforchange.co.uk/how-to-download-1xbet-app-for-convenient-betting/]http://www.accountingforchange.co.uk/how-to-download-1xbet-app-for-convenient-betting/[/url] or types of sports. in such games are used various themes, payment and bonus features.
Adamsonna Oct. 20, 2025, 8:20 p.m.
Фигурки кульные)))))) w dyspozycji graczy jest okolo 40 na zywo gier/ rozrywki od wiodacych dostawcow, [url=https://2020.colegio-santagema.es/hotline-casino-twoje-miejsce-na-emocjonujce-gry-2/]https://2020.colegio-santagema.es/hotline-casino-twoje-miejsce-na-emocjonujce-gry-2/[/url] jak evolution gaming i pragmatic play live.
MikeAcigo Oct. 20, 2025, 8:12 p.m.
Да, все логично Dalej popiseme rozhodujuce faktory, ktore ovplyvnili nase rozhodnutie.[url=https://protezsacumraniye.com/objavte-svet-online-kasin-zabava-a-vyhry-na-dosah/]https://protezsacumraniye.com/objavte-svet-online-kasin-zabava-a-vyhry-na-dosah/[/url] nepochybne napad platieb samozrejme musia byt uvedene v recenziach online kasin.
ArturoTig Oct. 20, 2025, 7:47 p.m.
Еще раз извините. Треки тоже бьются не сразу, курьерки "в завалах", иногда он только начинает определяться на сайте курьерки, а его уже вручают или вручили получателю. Не пугайтесь, что мониторинг начнется не сразу, вам всем все придет заказанное. <a href=https://amvrosievkaxy.ru>Закладки тут - купить гашиш, мефедрон, альфа-пвп</a> Какие обещания? если выходной, скорей всего СПРС в базу не завело твой трек, жди понедельника...
JenniferMet Oct. 20, 2025, 7:26 p.m.
live updates: real-time updates ensure users have access to the latest odds during live [url=https://buzzreleased.com/betwinner-11/]https://buzzreleased.com/betwinner-11/[/url] events.
zapojvladimirrix Oct. 20, 2025, 6:38 p.m.
В современном мире вопрос зависимостей становится все более актуальной. Если вы раздумываете о нарколога на дом в владимире, ресурс vivod-iz-zapoya-vladimir025.ru предлагает широкий спектр наркологических услуг. Лечение зависимостей может быть сложным процессом, однако мобильный нарколог предоставляет помощь при алкоголизме и другим зависимостям в домашних условиях. Консультация нарколога – это начальный этап к излечению. Квалифицированные специалисты проведут диагностику зависимости, помогут составить программу реабилитации и предложат методы психотерапии в рамках терапии. Конфиденциальное лечение гарантирует полную конфиденциальность, что особенно важно для многих пациентов. Выездная медицинская помощь позволяет не только проходить лечение в удобной обстановке, но и получать поддержку
ArturoTig Oct. 20, 2025, 6:06 p.m.
принимай не меньше 300 мг МХЕ от данного селлера. <a href=https://gorlovkati.ru>Приобрести MEF GASH SHIHSKI ALFA - ОТЗЫВЫ, ГАРАНТИИ, КАЧЕСТВО</a> МАГАЗИНУ надо бы по ровнее работать!
WendyEnubs Oct. 20, 2025, 5:54 p.m.
Professional sports leagues have renewed their own these are the for [url=https://i-wapp.es/imarkt/admin/descubre-el-mundo-del-juego-en-linea-con-betwinner/]https://i-wapp.es/imarkt/admin/descubre-el-mundo-del-juego-en-linea-con-betwinner/[/url] May 14 current year, when the Supreme Court of the USA repealed the act on the protection of special and amateur sports: since 1992 (paspa).
Stanleyinfib Oct. 20, 2025, 5:31 p.m.
1xBet промокод на сегодня 2026. Чтобы удовлетворить потребности бетторов и сделать процесс ставок максимально разнообразным нередко букмекерские конторы пытаются увеличить свой функционал, путем добавления специальных функций и предложений. Одним из лидеров среди популярных букмекеров на постсоветском пространстве по своим функциональным возможностям является 1хБет. Ввод <a href=https://www.kramatorsk.org/images/pages/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html >бесплатный промокод на 1хбет получить</a> позволяет получить увеличенную сумму бонуса. Для этого достаточно после создания аккаунта внести первый депозит (максимальная сумма бонусного начисления составляет 32500 рублей). Можно использовать любой платёжный метод. Абсолютно бесплатный промокод 1xBet. На сегодня к
Stevengug Oct. 20, 2025, 4:49 p.m.
Как купить A-PVP мука в Камень-на-Обие?Люди, помогите с выбором - есть вариант https://svco-group.ru . Цены вроде ок, доставляют. Кто-то сталкивался с ними? Как работают?
Laurentrak Oct. 20, 2025, 4:44 p.m.
we worried about, somehow there would be somethingsomething for everyone, including slot machines with three and five reels, blockbusters, like tomb Raider™, and in addition/in addition traditional [url=https://ayadina.78winn.net/discover-the-thrills-of-casiroom-online-casino-uk-5/]https://ayadina.78winn.net/discover-the-thrills-of-casiroom-online-casino-uk-5/[/url] blackjack and roulette.
Franksib Oct. 20, 2025, 4:40 p.m.
<a href=https://soskitum.info/girls/>индивидуалки в тюмени сейчас</a>
Ralphlox Oct. 20, 2025, 4:25 p.m.
<a href=https://potofu.me/8g0lynvr>https://potofu.me/8g0lynvr</a>
MikeCek Oct. 20, 2025, 2:49 p.m.
Вы не правы. Могу отстоять свою позицию. Пишите мне в PM, обсудим. Так, например, для моторов указанная частота может достигать 10 Гц, для цилиндров - до 7 Гц, а время, затрачиваемое мотором мощностью 3,75 кВт на реверс с частоты вращения 2500 1/мин и ассортимент этой скорости в противоположном направлении, составляет 0,02 с, что в некотором смысле на 2 порядка быстрее, <a href=https://www.dniproua.pp.ua/viewtopic.php?t=94>https://www.dniproua.pp.ua/viewtopic.php?t=94</a> нежели у асинхронного электродвигателя один и тот же мощности.
Stevengug Oct. 20, 2025, 2:28 p.m.
Как купить Метамфетамин в Назаровое?Друзья, подскажите с выбором - есть вариант https://lvhandbags.ru . По деньгам нормально, доставляют. Кто-то сталкивался с ними? Насколько надежно?
Stanleyinfib Oct. 20, 2025, 2:21 p.m.
Промокод 1xBet на сегодня можно получить прямо на сайте букмекерской компании. Сделать это станет возможным благодаря переходу по рабочей ссылке, содержащей промокод. Подобного рода бонусы могут использовать и постоянные и новые клиенты конторы. Благодаря проведению таких акций интерес игроков к ставкам остаётся высоким. Содержание. <a href=https://adok.ru/news/ph/?1xbet-promokod-pri-registracii-besplatno.html >1xbet промокод 6500 руб</a>. Как получить и что дает промокод в 1xBet? Где вводить промокод в 1xBet? Рабочие промокоды 1xBet на сегодня. Действующие промокоды 1xBet на сегодня. Узнайте как ввести промо код 1хБет при регистрации и получить 32500 рублей на бесплатную ставку. Как активировать и использовать промокод на 1xBet. Список рабочих бонус кодов.
Ralphlox Oct. 20, 2025, 1:02 p.m.
<a href=https://kemono.im/oheduafyhiby/kupit-akkumuliatornuiu-boshku>https://kemono.im/oheduafyhiby/kupit-akkumuliatornuiu-boshku</a>
Ernestvaria Oct. 20, 2025, 12:46 p.m.
<a href=https://dzen.ru/a/aPRYvcQ7DQpOXka7>виртуальный номер для банковских сервисов</a>
EpicksonMeamy Oct. 20, 2025, 12:45 p.m.
Огромное спасибо за объяснение, теперь я не допущу такой ошибки. Na Slovensku su hry such riadene regulacnym uradom sports betting (URHH), <a href=https://soul-mate.co.kr/57472/>https://soul-mate.co.kr/57472/</a>, ktora je podriadena Ministerstvu financii.
JamesFET Oct. 20, 2025, 12:26 p.m.
Промо-код 1xBet — пропишите его в специальное поле при создании аккаунта, пополните свой счет на сумму от 100 RUB и активируйте предложением в размере 100% (до 32 500 RUB). В личном кабинете отыщите раздел «Бонусы» и отметьте вариант «Ввести код». Введите полученный код в соответствующее поле. Активируйте и ознакомьтесь с условиями использования.Промокод 1xBet на 2026 год можно взять по ссылке — <a href=https://voronezhturbo.ru/images/pages/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html>https://voronezhturbo.ru/images/pages/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html</a>.
Stevengug Oct. 20, 2025, 12:06 p.m.
Как купить Атаракс в Гореловое?Заметил на сайт https://kernatoms.ru - судя по отзывам ок. По цене устроило, доставка есть. Кто-нибудь пробовал? Интересует качество?
LatricePap Oct. 20, 2025, 11:59 a.m.
for more versatile Getting to know this <a href=https://grooveart.es/explore-the-exciting-world-of-yummy-wins-casino-4/>https://grooveart.es/explore-the-exciting-world-of-yummy-wins-casino-4/</a> at cards, please check out our casino review of the Top 5.
Lawrencesat Oct. 20, 2025, 11:57 a.m.
ДА, вариант хороший na stronach portalu spotkasz ruletke online, blackjacka (w tym vip Blackjacka), Bakarata, lucky seven, <a href=https://b2b.holidaygolf.se/wspaniae-dowiadczenia-w-hotline-casino/>https://b2b.holidaygolf.se/wspaniae-dowiadczenia-w-hotline-casino/</a> dragon tiger ... hotline maksymalna odpowiednia dla wariantu inteligentnego? nie prosi do pobrania aplikacji.
vivodsmolenskrix Oct. 20, 2025, 11:53 a.m.
вывод из запоя цена <a href=https://vivod-iz-zapoya-smolensk024.ru>vivod-iz-zapoya-smolensk024.ru</a> вывод из запоя цена
KimInser Oct. 20, 2025, 11:13 a.m.
посмотрю што это и с чем ево едят {sexy|erotic|seductive|depraved} {girls|young ladies|dolls|beauties} on webcam. Thousands of free {porn actresses|sex models} showing {videos|videos|videos|files} on {your|your} {web cam|webcam} in {different|different} categories. nudelive {offers|provides|gives} you get free sex on a webcam like {no other {site|resource|portal} {18+|for adults}, {where|on which} {it is possible|possible|available|real} {to watch|find|discover} online #file_links<>C:\Users\Admin\Desktop\file\gsa+en+Phoenix40k80k150k300k979P2URLBB.txt",1,N].
Marvinseala Oct. 20, 2025, 11 a.m.
Le code promotionnel n'est pas necessaire : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu'a 130€, pour vos paris sportifs. Vous pouvez vous inscrire sur le site 1xBet ou via l'application mobile. Apres votre premier depot, vous activerez le code bonus. L'offre est valable pour toute l'annee 2026, et le bonus doit etre mise dans les 30 jours. Vous pouvez trouver le code promo sur ce lien — <a href=https://www.stella-charlott-roth.de/wp-content/pgs/22le-code-promo-1xbet_bonus.html>https://www.stella-charlott-roth.de/wp-content/pgs/22le-code-promo-1xbet_bonus.html </a>.
Stevengug Oct. 20, 2025, 10:57 a.m.
Подскажите, стоит ли заказывать на https://maksp.ru ? Цены привлекательные, есть доставка. Хочу узнать про реальное качество.
Stanleyinfib Oct. 20, 2025, 10:51 a.m.
Воспользоваться промокодом 1xBet можно при регистрации в 1xBet. БК 1хБет дарит до 125% на первый депозит при помощи промокода 1xBet. Максимальная сумма бонуса по промокоду 1хБет достигает 32500 рублей. Промокод 1хБет дает надбавку на депозит до 125% только при первом пополнении. Регистрация. <a href=https://spectehmontazh.ru/uploads/pgs/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html >списки промокодов на 1xbet</a>. Всем известно, что букмекерская контора 1xBet предлагает широкий выбор разнообразных бонусов и акций. В этой статье мы расскажем все о промокодах 1xBet: что это, как использовать при регистрации, где вводить, чтобы сделать ставку бесплатно, и по каким поводам казахстанский букмекер 1хБет вручает именные промокоды. Содержание. Что такое промокод 1xBet. Бесплатны
AnthonyRax Oct. 20, 2025, 9:37 a.m.
https://imageevent.com/syifaharuka7/xswbn
Markfearm Oct. 20, 2025, 9:36 a.m.
Сторонники данного подхода считают, что феномены человеческого поведения, <a href=https://malhamad.net/exploring-the-future-of-swipey-ai-sex-bridging/>https://malhamad.net/exploring-the-future-of-swipey-ai-sex-bridging/</a> его способность к занятиям и адаптации есть следствие именно биологической структуры и особенностей её функционирования.
JamesFET Oct. 20, 2025, 8:34 a.m.
1xBet бонусный код на приветственный бонус в 2026 году — введите промокод и активируйте бонус в размере 100% до 100$. Специальный промокод позволяет получить увеличенный стартовый бонус от БК 1xBet после создания аккаунта. Промокод всегда доступен по ссылке ниже — <a href=https://voronezhturbo.ru/images/pages/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html>https://voronezhturbo.ru/images/pages/?1xbet_promokod_pri_registracii_na_segodnya_besplatno.html</a>.
Marvinseala Oct. 20, 2025, 8:31 a.m.
Offre promotionnelle 1xBet pour 2026 : recevez une offre de 100% jusqu’a 130€ lors de votre inscription. Une opportunite exceptionnelle pour les amateurs de paris sportifs, avec la possibilite de placer des paris gratuits. Inscrivez-vous avant la fin de l’annee 2026. Decouvrez le code promotionnel 1xBet via le lien fourni — <a href=https://www.stella-charlott-roth.de/wp-content/pgs/22le-code-promo-1xbet_bonus.html>Un Code Promo X Bet</a>. Le code promo 1xBet vous permet d’activer un bonus d’inscription 1xBet exclusif et de commencer a parier avec un avantage. Le code promotionnel 1xBet 2026 est valable pour les paris sportifs, le casino en ligne et les tours gratuits. Decouvrez des aujourd’hui le meilleur code promo 1xBet et profitez du bonus de bienvenue 1xBet sans depot initial.
AnthonyRax Oct. 20, 2025, 7:56 a.m.
https://rant.li/acqoyfaecsu/kupit-geroin-nedorogo
Stevengug Oct. 20, 2025, 7:23 a.m.
Смотрите, нашел https://timetodrink.ru - ценник адекватный, доставка быстрая. Кто-то пробовал у них? Как с качеством продукции?
Stanleyinfib Oct. 20, 2025, 7:03 a.m.
Сайт 1xBet считается одним из самых надежных онлайн букмекеров России. БК 1xBet пользуется огромной популярностью среди пользователей из РФ и стран СНГ. Лучшие коэффициенты ставок на спорт, лучшие онлайн игры, слоты казино и еще много других плюсов букмекерской конторы заслуживают внимания. <a href=https://provisorclub.com/content/pags/1xbet-promokod-pri-registracii-besplatno.html >1xbet промокод при регистрации на сегодня</a>. Для постоянных игроков БК 1хБет регулярно проводятся различные акции, в рамках которых любая положенная на счет сумма (в рамках определенных пределов) будет увеличена (обычно в два раза). Для вывода подарочных денег требуется поставить деньги несколько раз на события с определенными условиями. Ставки на спорт 2026 - Получить бонус 1xBet и промокод на 32500 руб
vivodkrasnodarrix Oct. 20, 2025, 6:37 a.m.
лечение запоя <a href=https://narkolog-krasnodar016.ru>narkolog-krasnodar016.ru</a> вывод из запоя краснодар
AnthonyRax Oct. 20, 2025, 6:15 a.m.
https://wirtube.de/a/wilson_margarete75863/video-channels
Marvinseala Oct. 20, 2025, 6:08 a.m.
Le code promo est supprime : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu'a 130€, a utiliser dans les paris sportifs. Inscrivez-vous sur 1xBet ou via l'application mobile. Apres votre premier depot, vous activerez le code bonus. L'offre est valable pour toute l'annee 2026, et le bonus doit etre mise dans les 30 jours. Decouvrez plus d'informations sur le code promo via ce lien — <a href=https://www.freie-waehler-werdau.de/wp-content/pgs/le-code-promo-1xbet_bonus.html>1xbet Bonus De Bienvenue 2026</a>. Le code promo 1xBet casino offre des tours gratuits et un bonus de depot 1xBet pour les nouveaux joueurs. Avec le code promotionnel 1xBet pour nouveaux utilisateurs, recevez jusqu’a 130€ de bonus d’inscription 1xBet. Utilisez le code promo 1x
MadelineHek Oct. 20, 2025, 5:53 a.m.
players from Ukraine, Russia, betwinner <a href=https://sppp.socsci.uva.nl/archives/1615650>https://sppp.socsci.uva.nl/archives/1615650</a> and Belarus are able to use portal, which is multilingual. smartphone application supports all devices with iOS and android operating systems.
HeatherTen Oct. 20, 2025, 5:13 a.m.
Извиняюсь, ничем не могу помочь, но уверен, что Вам помогут найти правильное решение. Не отчаивайтесь. Bankove prevody vam umoznuju manipulovat s velkymi financnymi sumami, <a href=https://www.oawm.com/kasina-s-vkladom-paypal-vetko-o-potrebujete-vedie-5/>https://www.oawm.com/kasina-s-vkladom-paypal-vetko-o-potrebujete-vedie-5/</a>ale velmi doplnenie uctu, nikdy vybery su pomale Proti inych metod.
avenue17 Nov. 18, 2023, 4:01 a.m.
There is a site, with an information large quantity on a theme interesting you.
Can Benli June 20, 2023, 9:05 a.m.
Harika anlatım.